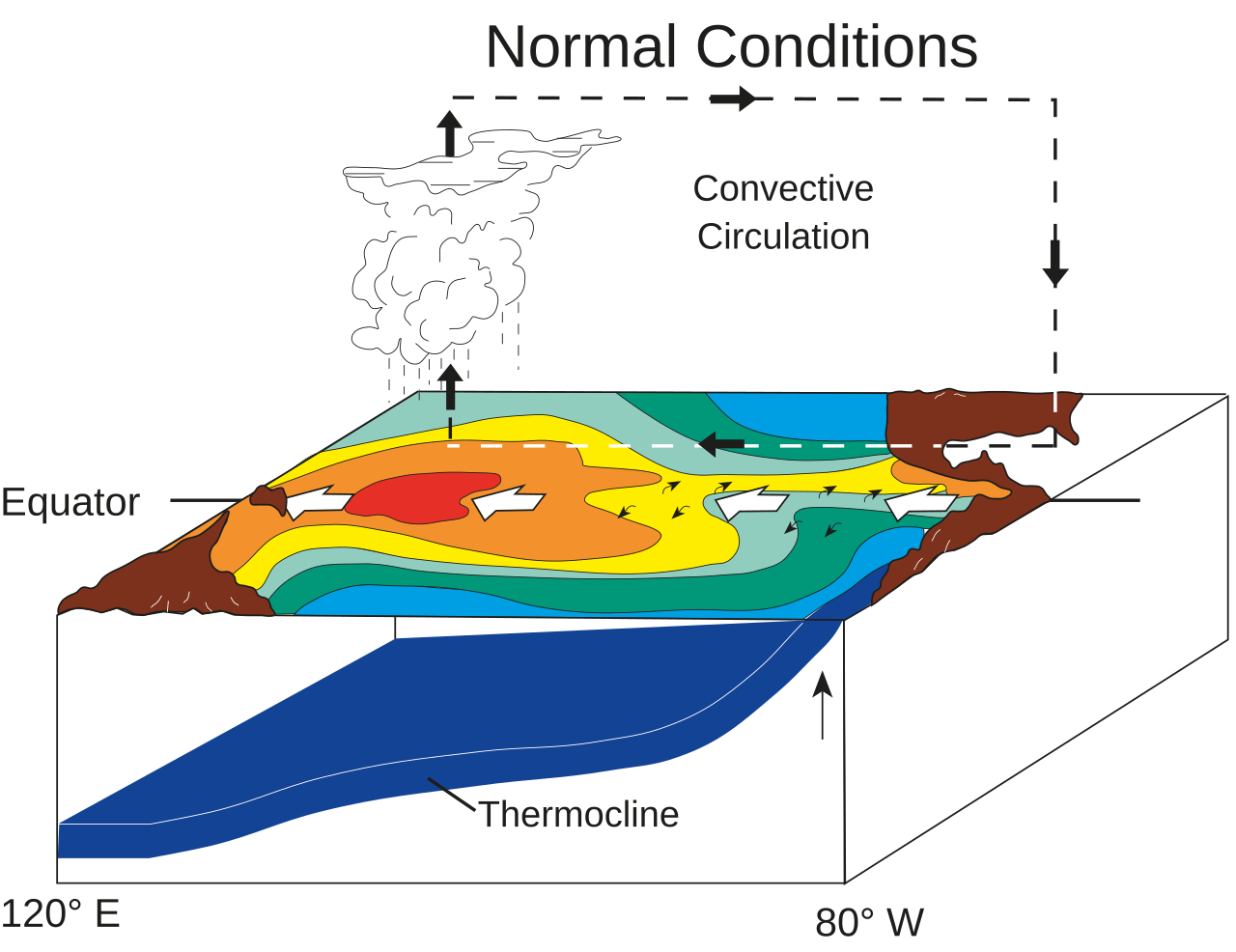
Zirkulation im tropischen Südpazifik.
[https://en.wikipedia.org/wiki/El_Ni%C3%B1o%E2%80%93Southern_Oscillation#/media/File:ENSO_-_normal.svg]

Wir hatten in der letzten Vorlesung die Betrachtung der stationären Meeresströmungen abgeschlossen und uns zeitlich veränderlichen Phänomenen zugewendet. Zwei weitere wollen wir heute noch ansehen, nämlich die El Niño Southern Oscillation (ENSO) im tropischen Südpazifik und die Atlantic Meridional Overturning Circulation (AMOC) im nördlichen Atlantik.
Im tropischen Südpazifik gibt es einen klassischen “subtropical gyre”, wie wir ihn schon behandelt haben. An dessen Ostrand (an der südamerikanischen Westküste) gibt es besonders kaltes Wasser, da die Küste Perus in Südost-Nordwest-Richtung verläuft genau wie der Passatwind. Das führt zu Küstenauftrieb.
Das Ergebnis ist, dass es normalerweise einen ausgeprägten Ost-West-Temperaturgradienten gibt, der aufgrund der Größe des Pazifik auch starke meteorologische Auswirkungen hat. Das warme Wasser führt zu aufsteigender Luft und viel Regen über Südostasien und absinkender Luft über Südamerika, so dass eine atmosphärische Zirkulation entlang der Breitenkreise entsteht. Dies ist die Walker-Zirkulation.

In unregelmäßigen Abständen, etwa alle 4-7 Jahre, kommt es aber vor, dass eine äquatoriale Kelvinwelle losläuft und ostwärts Downwelling exportiert. Im Effekt wird das Upwelling an der Küste Südamerikas reduziert. Das Wasser wird wärmer und die aufsteigenden Luftmassen verlagern sich ostwärts.
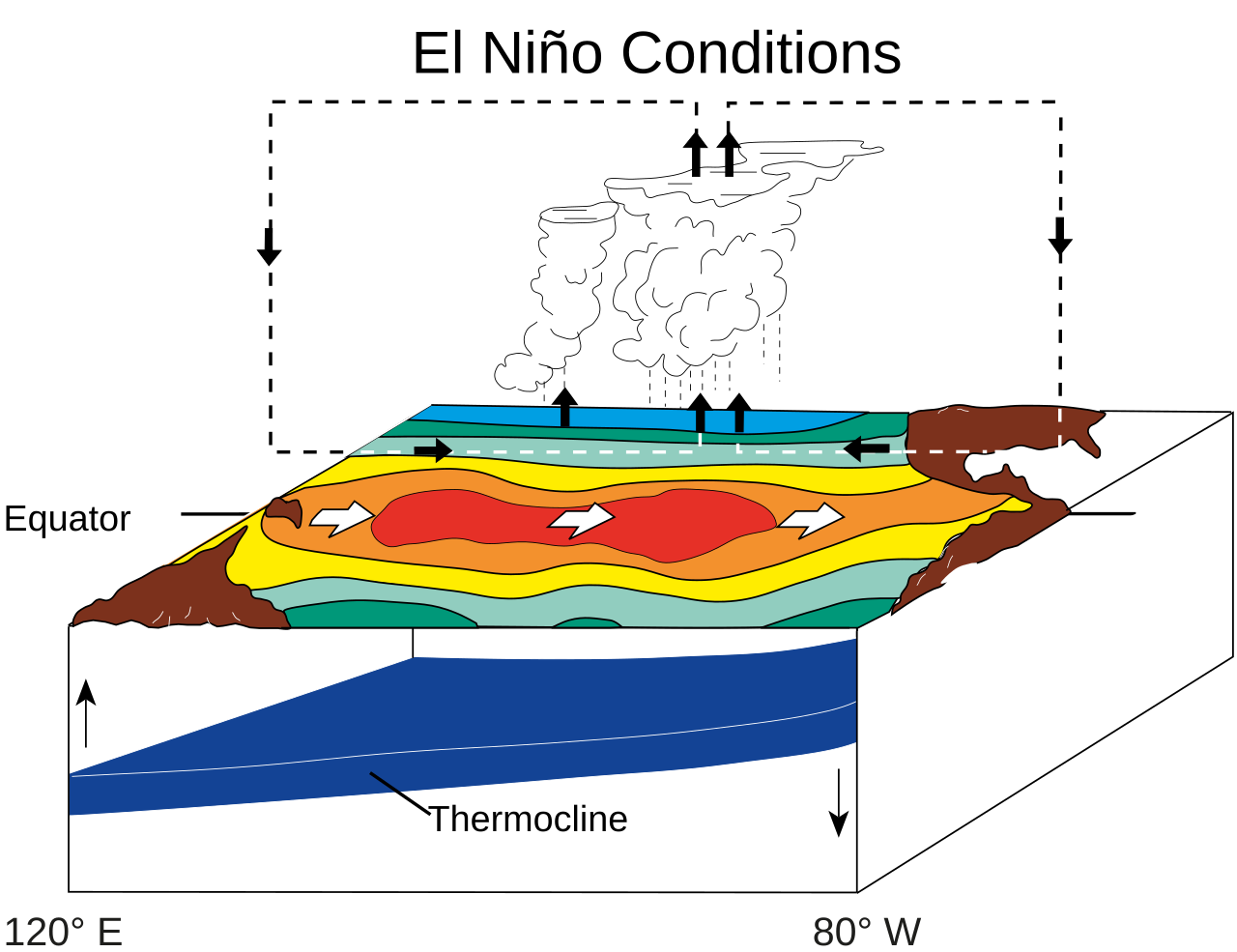
Die Folge in Südostasien sind Dürren wegen des ausbleibenden Niederschlags. Die Folge in Südamerika ist ein Ausbleiben von Fischschwärmen, aufgrund der hohen Temperaturen, und weil der Auftrieb von Nährstoffen mit dem Tiefenwasser fehlt. Weil dieser Effekt meist um die Weihnachtszeit spürbar wird, wird das Phänomen von den dortigen Fischern “El Niño” (das Christkind) genannt. Die damit verbundene Variabilität in der atmosphärischen Zirkulation wird “Southern Oscillation” genannt.
Aufgrund der verheerenden ökonomischen Auswirkungen besteht erhebliches Interesse daran, das Auftreten von El-Niño-Jahren vorherzusagen. Der genaue auslösende Mechanismus ist aber noch nicht gut genug verstanden, um eine seriöse Vorhersage zu ermöglichen.
Vermutet wird, dass die Intensität der El-Niño-Ereignisse mit dem Klimawandel zunimmt. Sicher ist, dass die globalen Erwärmung die Ökosysteme an der südamerikanischen Küste verwundbarer macht für eine zusätzliche Erwärmung durch El Niño.
Eine Strömung, die man eigentlich für eine stationäre Strömung hielt, die sich aber verändert, ist die Atlantic Meridional Overturning Circulation (AMOC).
Der Golfstrom teilt sich vor der europäischen Küste auf in einen südlichen Ast (der den “subtropical gyre” schließt) und einen nördlichen Ast, der ins Nordpolarmeer strömt. Das warme Wasser trifft dort auf kalte Atmosphärentemperaturen, was zu hoher Verdunstung führt, und danach und dadurch auch zu Abkühlung. Das kalte und salzhaltige Wasser sinkt aufgrund seiner hohen Dichte ab und fließt im Tiefenozean nach Süden zurück.
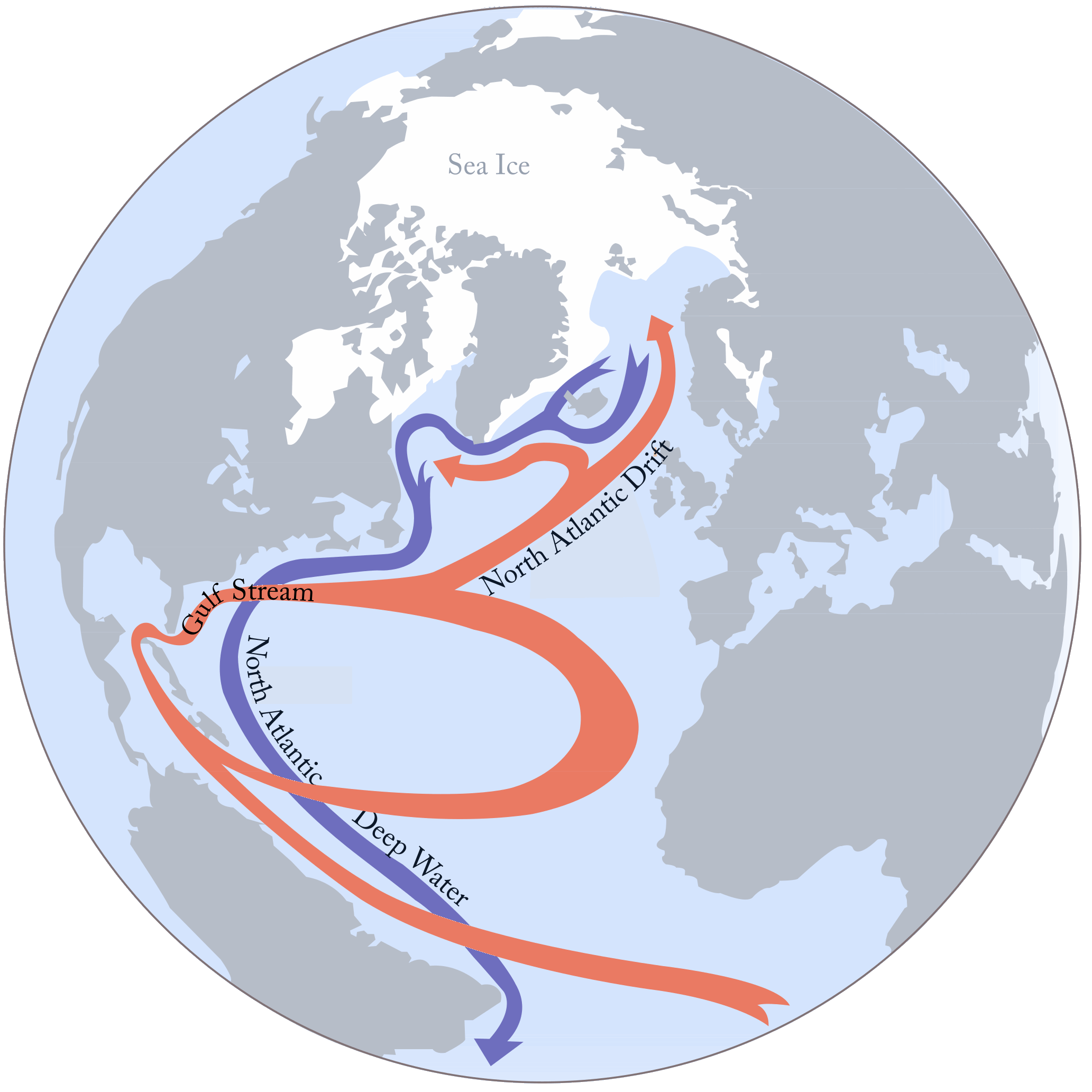
Man kann im Atlantik die nordwärtige Oberflächenströmung messen. Dies geschieht bei 26,5°N mit zwei Methoden.
Zwischen Florida und den Bahamas ist ein Seekabel auf dem Grund verlegt. Da der starke und schnelle Florida-Strom darüber fließt, wir durch das Erdmagnetfeld im Kabel eine Spannung induziert. Die Ursache ist, dass sich das Salzwasser als elektrischer Leiter relativ zum Magnetfeld bewegt. Aus der Spannung kann man den Transport im Floridastrom ableiten.
Für den Transport weiter östlich im Rest des Atlantik wurde eine Reihe von Moorings installiert, das “RAPID array”. Mithilfe dieser kann man verschiedene Anteile der nordwärtigen Oberflächenströmung berechnen, zum Beispiel den Ekman-Transport-Anteil und den geostrophischen Anteil.

Was sich zeigt, ist, dass die Stärke dieser nordwärtigen Strömung abgenommen hat, von ca. 20 Sv in den 1990er Jahren auf nur noch um die 14 Sv heute. Messungen und zugehörige Satellitenanalysen liefern hier dasselbe Ergebnis.

Man nimmt an, dass die Ursache das Schmelzen des arktischen und Grönländischen Eises ist. Das Schmelzwasser verdünnt das Meerwasser, dieses ist zwar noch kalt, aber weniger salzig als zuvor. Daher wird sein Absinken gehemmt.
Klimaszenarien gehen davon aus, dass sich die Zirkulation weiter abschwächen wird, ein kompletter Abbruch der Zirkulation bis 2100 aber unwahrscheinlich ist. Diese Einschätzung ist im IPCC-Report mit “medium confidence” angegeben. Ein Abbruch der Zirkulation hätte dramatische klimatische Folgen für Europa. Er würde zu einer Abkühlung Skandinaviens und Nordeuropas führen, die stärker als die globale Erwärmung ist.
Dabei bliebe der windgetriebene Anteil des Golfstroms unverändert, aber der durch die thermohaline Zirkulation angetriebene würde sinken.
Ästuare sind Gebiete an der Küste des Meeres, in denen sich Flusswasser und Meerwasser mischen. Sie sind also durch Brackwasser gekennzeichnet. In ein Ästuar können ein oder mehrere Flüsse münden.
Auch die Ostsee hat Eigenschaften eines großen Ästuars. Sie hat aber aufgrund ihrer Größe auch Eigenschaften, die man eher in Meeren findet. So ist sie in zahlreiche Becken zergliedert und in ihrem Innern über 200 m tief. Auch ist ihre Nord-Süd-Ausdehnung so groß, dass sie sich über verschiedene Klimazonen erstreckt (gemäßigtes und subpolares Klima).
Ästuare werden nach ihrer Form typischerweise in drei Arten unterschieden.
trichterförmige Gezeitenästuare
In Gebieten mit hohem Tidenhub, wie der Nordsee, bilden sich trichterförmige Ästuare. Die Erosion durch die starken Gezeitenströmungen dominiert hier am seeseitigen Rand des Ästuars.

Deltas
In Gebieten mit geringem oder ohne Tidenhub bilden sich Mündungsdeltas, in denen sich der Fluss dreiecksförmig in verschiedene Mündungsarme auffächert. Hier dominiert die Sedimentation der im Fluss mitgeführten Schwebstoffe, der zu einer Verlandung führt. Streng genommen bildet nur der seewärtige Teil des Deltas, in dem Brackwasser eindringen kann, das Ästuar. Ein Beispiel ist das Amazonasdelta, in dem der wasserreichste Fluss der Erde in den Atlantik mündet.

Lagunen
An sandigen Küsten ist die Morphodynamik (die Änderung der Meerestiefe durch Erosion und Sedimentation) oft vom küstenparallelen Transport von Sand bestimmt. Hier bilden sich lagunenförmige Ästuare. Beispiele aus der Ostsee wären das Oderhaff oder das Kurische Haff.

Die Residenzzeit beschreibt, wie lange ein Wasserpaket, das in ein Meeresgebiet gelangt, durchschnittlich darin bleibt, bis es dieses Gebiet erstmalig wieder verlässt. Es beschreibt also die mittlere Dauer, die es braucht, das Wasser im Gebiet durch neues Wasser von außen zu ersetzen.
Im Gegensatz zur “residence time” gibt es noch die “influence time”. Während man die “residence time” auffhört zu zählen, wenn das Wasserpaket erstmalig raus ist aus dem Gebiet, zählt man die “influence time” weiter, wenn das Wasserpaket später nochmal wiederkommt. Gerade bei gezeitendominierten Systemen, wo man immer wieder Ein- und Ausstrom hat, ist das relevant.
“residence time” und “influence time” sind wichtige Größen wenn es um angewandte Fragen geht. Zum Beispiel, wie schnell sich ein Meeresgebiet nach einer Freisetzung von Schadstoffen erholen kann. In Ästuaren ist die Residenzzeit auch entscheidend für biologische Umsätze. Ästuare wirken für das angrenzende Meer wie große Klärwerke und entfernen einen erheblichen Teil der mit den Flüssen eingetragenen Nährstoffe.
Wenn man annimmt, dass das Volumen eines Ästuars konstant bleibt, kann man die Residenzzeit einfach ausrechnen.
\[ t_r = \frac{V}{Q_{in}} = \frac{V}{Q_{out}} \]
Man dividiert also das Volumen des Ästuars durch die Rate des einströmenden oder ausströmenden Wassers in m³/s (die sind dann ja beide gleich). Wichtig hierbei ist, dass man nicht nur den Einstrom des Flusswassers nimmt. Denn es strömt ja auch vom Meer her Meerwasser ein, das sich mit dem Flusswasser mischt. Wieviel, ist oft schwer zu messen, denn das kann ja zeitlich stark schwanken, und man ist meist an einem Mittelwert interessiert.
Daher hat sich schon im 19. Jahrhundert eine Methode etabliert, wie man die Menge des vom Meer her einströmenden Wassers nur aus Messungen des Salzgehaltes bestimmen kann, wenn man die Abflussrate des Flusses kennt. Diese Methode ist als Knudsen-Theorem bekannt.
Wir wollen nun ausrechnen, wie lange Wasser durchschnittlich im Oderhaff verbleibt.
Das Volumen des Oderhaffs beträgt \(V = 2,6\) km³ = 2 600 000 000 m³. Der Ausstrom der Oder beträgt \(Q_r = 710\) m³/s. Kleinere Flüsse wie Peene und Uecker können wir vernachlässigen. Würde also nur das Oderwasser durch das Oderhaff fließen, würde es eine Residenzzeit von
\[ t_r = \frac{V}{Q_r} = 3.661\cdot 10^6\, \mathrm{s} = 42\, d \]
also 42 Tagen haben.
Allerdings verkürzt sich diese Zeit, denn wir haben auch noch Einstrom von der Ostsee her. Je größer \(Q_1\) und \(Q_2\) in der folgenden Grafik sind, um so schneller tauscht sich das Wasser aus.
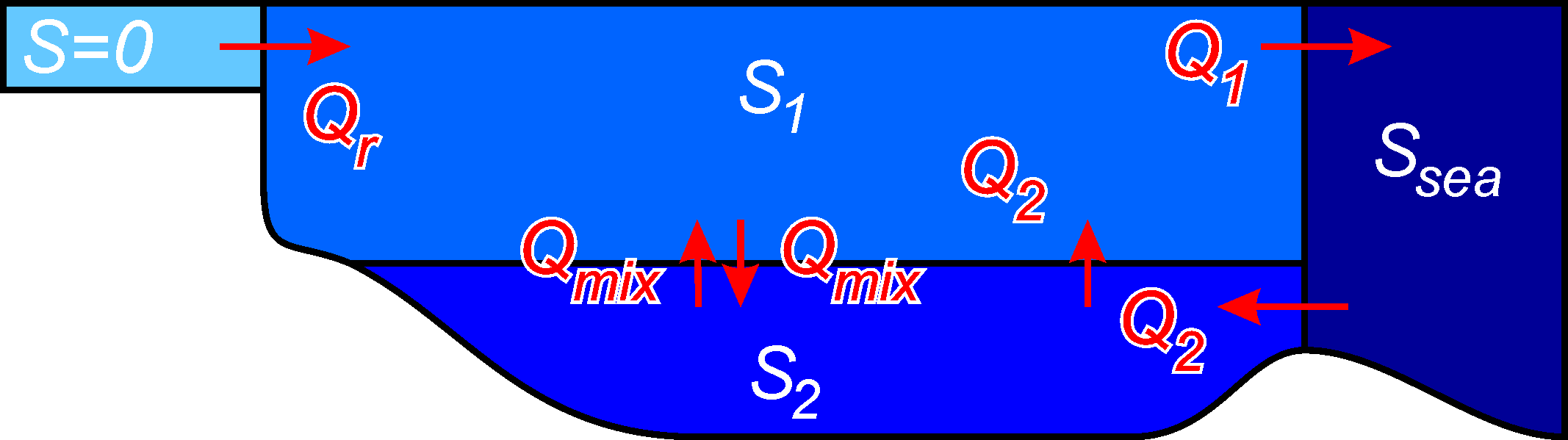
Diesen Austausch können wir nach dem Knudsen-Theorem aus den Salzgehalten ausrechnen. Dieses nimmt an, dass die Salzgehalte in der Oberflächen- und Bodenschicht konstant bleiben, weil sie im Gleichgewicht sind. Im Oderhaff haben wir etwa
\[ S_1 = 0.5\, \mathrm{g} \, \mathrm{kg}^{-1} \] \[ S_2 = 2\, \mathrm{g} \, \mathrm{kg}^{-1} \] \[ S_{sea} = 7\, \mathrm{g} \, \mathrm{kg}^{-1} \]
wobei \(S_{sea}\) hier den Salzgehalt in der Pommerschen Bucht beschreibt.
Ebenso nehmen wir an, dass das Volumen der beiden Wasserkörper konstant bleibt.
Wir können nun ein paar Gleichungen aufstellen. Zunächst mal eine Volumenbilanz, einströmendes und ausströmendes Volumen müssen gleich sein in der gesamten Bucht.
\[ Q_r + Q_2 = Q_1 \tag{1}\]
Dann die Salzbilanz für die obere Schicht, einströmende und ausströmende Salzmenge müssen gleich sein.
\[ Q_{mix} S_2 + Q_2 S_2 = Q_{mix} S_1 + Q_1 S_1 \tag{2}\]
Schließlich die Salzbilanz für die untere Schicht:
\[ Q_{mix} S_1 + Q_2 S_{sea} = Q_{mix} S_2 + Q_2 S_2 \tag{3}\]
Die Gleichungen können wir ineinander einsetzen. Wir nutzen die Volumenbilanz (1) , um in Gleichung (2) \(Q_1\) durch \(Q_r + Q_2\) zu ersetzen:
\[ Q_{mix} S_2 + Q_2 S_2 = Q_{mix} S_1 + Q_r S_1 + Q_2 S_1 \]
Wenn wir \(Q_{mix} S_1\) abziehen, ergibt sich
\[ Q_{mix} (S_2 - S_1) + Q_2 S_2 = Q_r S_1 + Q_2 S_1 \tag{4}\]
Nun wenden wir uns der Gleichung (3) zu. Da subtrahieren wir \(Q_{mix} S_1\):
\[ Q_2 S_{sea} = Q_{mix} (S_2 - S_1) + Q_2 S_2 \]
Den Term mit auf der rechten Seite haben wir gerade ausgerechnet in Gleichung (4). Wir können ihn einsetzen:
\[ Q_2 S_{sea} = Q_r S_1 + Q_2 S_1 \]
Wir subtrahieren \(Q_2 S_1\):
\[ Q_2 (S_{sea} - S_1) = Q_r S_1 \]
Wenn wir dividieren, können wir herausfinden, wie viel Volumen vom Meer her in die untere Schicht einströmt:
\[ Q_2 = \frac{Q_r S_1}{S_{sea} - S_1} \]
Offenbar haben wir den Wert für \(S_2\) gar nicht gebraucht.
Wir setzen mal unsere Werte ein:
\[ Q_2 = \frac{710 \, \mathrm{m}^3 \, \mathrm{s}^{-1} \cdot 0.5\, \mathrm{g} \, \mathrm{kg}^{-1}}{7\, \mathrm{g} \, \mathrm{kg}^{-1} - 0.5\, \mathrm{g} \, \mathrm{kg}^{-1}} = 54.6 \, \mathrm{m}^3 \, \mathrm{s}^{-1}\]
Zu den 710 m³/s aus der Oder kommen also noch weitere 55 m³/s aus dem Meer hinzu. Die Residenzzeit verkürzt sich entsprechend:
\[ t_r = \frac{V}{Q_r + Q_2} = 3.399\cdot 10^6\, \mathrm{s} = 39\, d \]
Die gleiche Methode kann man auch anwenden, wenn man ein langgestrecktes Ästuar hat, in dem sich die Salzgehalte entlang des Ästuars ändern. Hier fängt man von der Flussseite her an und berechnet die Bilanz für die ersten zwei Boxen. Dann kann man das Verfahren in Mündungsrichtung hin fortsetzen und immer die Flüsse in die nächsten zwei Boxen ausrechnen. Alles was man kennen muss, sind die Salzgehalte und der Abfluss des Flusses.
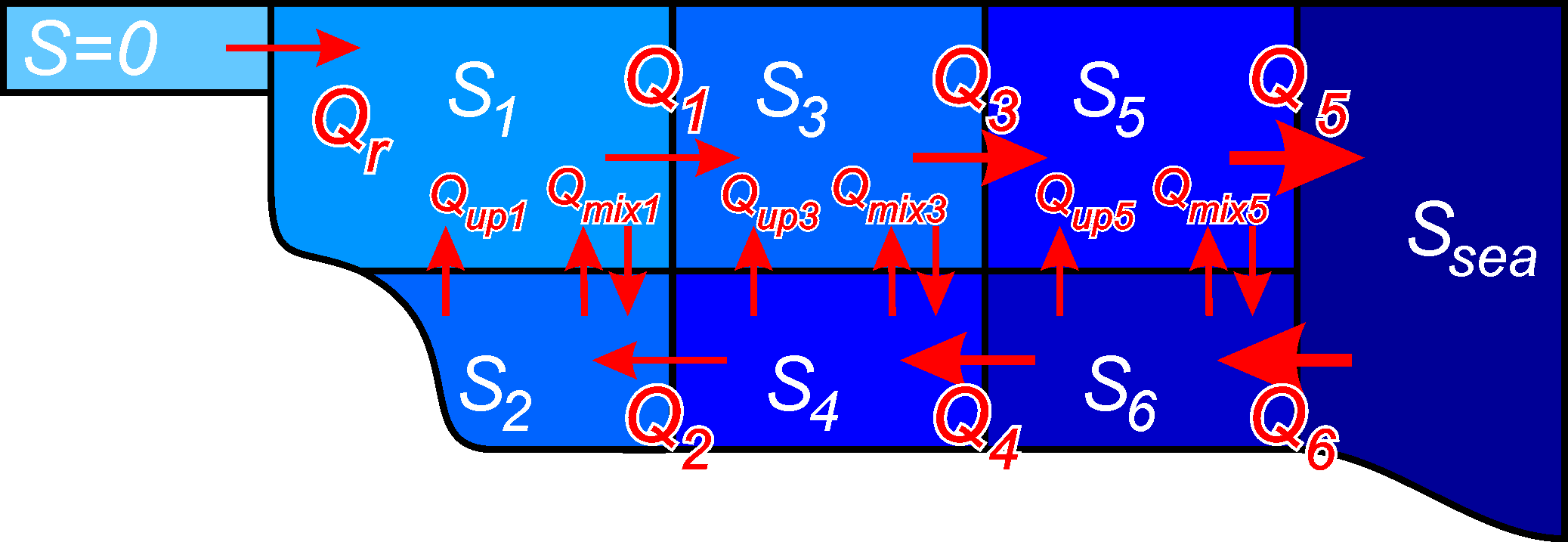
Das Entscheidende ist hier, dass der Tiefenwassereinstrom in Mündungsrichtung immer weiter zunimmt. Während er im Fall des Oderhaffs noch eher klein war, ist er z.B. im Elbe-Ästuar viel größer als der Frischwasserzustrom. Das ist auch die Take-Home-Message: Während relativ abgeschlossene, lagunenartige Ästuare vom Fluss dominiert sind, ist in offenen Ästuaren die ästuarine Zirkulation das Entscheidende für den Wassermassenaustausch. Sie bestimmt dann auch die Residenzzeit, die viel kürzer ist, als die Abflussrate des Flusses das vermuten lässt.