
Cold-core Eddy (links) und Warm-core Eddy (rechts).
[https://www.researchgate.net/publication/353382761/figure/fig1/AS:1048379136155654@1626964472822/a-Cyclonic-eddy-and-b-anticyclonic-eddy-three-dimensional-schematic-diagram-Shades.png]

In der letzten Vorlesung haben wir das Prinzip der Geostrophie kennengelernt, nun wollen wir es anwenden. Als Beispiel wollen wir gemäß der “dynamischen Methode” die Strömung zwischen zwei Stationen ausrechnen.
Wir haben an zwei Stationen im Meer die Dichte bestimmt. Wir nehmen vereinfachend an, dass am ersten Punkt die Dichte konstant mit \(\rho_1\) und am zweiten Punkt konstant mit \(\rho_2\) ist. Der Meeresboden zwischen den beiden Punkten soll der Einfachheit halber flach sein.
Um die geostrophische Strömung aus der Dichte zu berechnen, gehen wir von der Annahme aus, dass der Druckgradient am flachen Boden verschwindet, d.h. der Druck \(p\) am Boden soll derselbe sein.
Die Berechnung erfolgt in mehreren Schritten, beginnend mit der Anwendung der hydrostatischen Näherung. Die hydrostatische Näherung besagt, dass der Druck in einer Flüssigkeit aufgrund des Gewichts der darüber liegenden Flüssigkeitssäule entsteht. An Punkt 1 gilt am Boden:
\[ p = \rho_1 \cdot g \cdot H_1 \]
und an Punkt 2 gilt am Boden:
\[ p = \rho_2 \cdot g \cdot H_2 \]
Wir sagen, dass \(H\) die Tiefe des Bodens ist und an Punkt 1 das Wasser genau diese Tiefe hat, \(H_1 = H\). Wir nehmen mal an, 300 m. An Punkt 2 kommt ein Wasserstand \(\eta\) dazu, \(H_2 = H + \eta\).
Wir arbeiten mit folgenden Werten:
\[ H = 300\,\mathrm{m} \] \[ \rho_1 = 1025\,\mathrm{kg/m}^3 \] \[ \rho_2 = 1024\,\mathrm{kg/m}^3 \] \[ \Delta x = 10\,000\,m \] \[ g = 9.81\,\mathrm{m/s}^2 \] \[ f = 1\cdot 10^{-4}\,\mathrm{s}^{-1} \]
Wir berechnen erstmal den Druck \(p\):
\[ p = \rho_1 \cdot g \cdot H = 3\, 016\, 575 \,\mathrm{Pa} \]
Damit können wir umgekehrt \(H_2\) ausrechnen:
\[ H_2 = \frac{p}{\rho_2 g} = 300.292\,\mathrm{m} \]
Wir haben also eine Wasserstandsdifferenz von
\[ \eta = H_2 - H = 0.292\,\mathrm{m} \]
In der Tiefe \(z=0\) ergibt sich an Station 2 folgender Druck:
\[ p_\eta = \rho_2 \cdot g \cdot \eta = 2934\,\mathrm{Pa} \]
Die Druckgradientenkraft ergibt sich als
\[ \frac{\Delta p}{\Delta x} = 0.2934\,\mathrm{N/m}^3 \]
Wenn wir vereinfachend annehmen, dass der Wasserstand zwischen den beiden Stationen linear verläuft, entspricht das auch der Ableitung:
\[ \frac{\partial p}{\partial x} = 0.2934\,\mathrm{N/m}^3 \]
Daraus können wir mit der Formel aus der letzten Vorlesung die Strömung quer zum Gradienten ausrechnen:
\[ v = \frac{1}{f \cdot \rho} \frac{\partial p}{\partial x} = \frac{1}{ 1\cdot 10^{-4}\,\mathrm{s}^{-1} \cdot 1024\,\mathrm{kg/m}^3} \cdot 0.2934\,\mathrm{N/m}^3 = 0.72\,\mathrm{m/s} \]
Das Wasser strömt also mit einer Geschwindigkeit von 0.72 m/s nordwärts. (Zum Herleiten der Einheit muss man beachten, dass 1 N = 1 kg m/s² .)
Dies ist aber nur an der Oberfläche so, da die Isobaren mit der Tiefe immer weniger geneigt sind und am Boden horizontal verlaufen, nimmt auch die Strömung linear mit der Tiefe ab, bis sie am Meeresboden null ist. Die mittlere Strömung ist also nur halb so groß, 0.36 m/s.
Um den Transport auszurechnen, müssen wir nun noch mit der Wassertiefe und der Breite multiplizieren:
\[ Q = v \cdot H \cdot \Delta x = 1.08\cdot 10^6\,\mathrm{m}^3\mathrm{/s} \]
Das wird in der Ozeanographie auch als 1.08 Sv (=Sverdrup) bezeichnet (1 Sv = 1 Million m³/s).
Hier einige starke Meeresströmungen:
| Strömung | Stärke |
|---|---|
| Antarktischer Zirkumpolarstrom | 125-150 Sv |
| Golfstrom | 30-150 Sv |
| Kuroshio-Strom | 50-70 Sv |
| AMOC (Absinkendes Wasser im arktischen Nordatlantik) | 15 Sv |
| —————————————————- | ———- |
| zum Verleich: Amazonas | 0.39 Sv |
Eine gute Anlaufstation, wenn man ozeanographische Daten braucht, ist das Copernicus-Datenportal der EU:
Da gibt es verschiedene Datenprodukte, die man sich visualisieren oder auch herunterladen kann. Es sind physikalische und chemische Parameter zu finden. Die Daten stammen meist aus Satellitenbeobachtungen oder Modellierung.
Wenn wir eine Visualisierung der Strömung ansehen, zeigt sich, dass viel Dynamik herrscht. Statt stationärer Strömungen sehen wir insbesondere viele Wirbel.
Daher wollen wir uns zunächst mit Wirbeln beschäftigen. Wir lernen,
wie man Wirbel beschreibt,
wie die Geostrophie Wirbel stabil macht,
warum Meeresströmungen Wirbel erzeugen.
Wirbel im Ozean werden auch mit ihrem englischen Begriff “Eddy” bezeichnet.
Die Strömung in einem Wirbel ist durch Rotation gekennzeichnet, d.h. das Wasser dreht sich um eine Achse.
Die Rotation in einem Stromfeld können wir ausrechnen, indem wir das Kreuzprodukt mit dem Nabla-Operator bilden. Das ergibt einen Vektor, dessen Richtung die Drehachse anzeigt.
\[ \textrm{rot}\,\vec{u} = \vec{\nabla}\times\vec{u} \]
Wir rechnen das mal aus:
\[ \vec{\nabla}\times\vec{u} = \begin{pmatrix} \frac{\partial}{\partial x} \\ \frac{\partial}{\partial y} \\ \frac{\partial}{\partial z} \end{pmatrix} \times \begin{pmatrix} u \\ v \\ w \end{pmatrix} = \begin{pmatrix} \frac{\partial w}{\partial y} - \frac{\partial v}{\partial z} \\ \frac{\partial u}{\partial z} - \frac{\partial w}{\partial x} \\ \frac{\partial v}{\partial x} - \frac{\partial u}{\partial y} \end{pmatrix} \]
Da sich Wirbel um die vertikale Achse drehen, sind wir an der \(z\)-Komponente interessiert. Die bezeichnen wir als Vorticity oder Wirbelstärke (veraltet: Trudelwucht).
\[ \zeta = \frac{\partial v}{\partial x} - \frac{\partial u}{\partial y} \]
Diese Größe entspricht der doppelten Winkelgeschwindigkeit:
\[ \zeta = 2 \omega \]
Positive Werte von \(\zeta\) bedeuten, dass ein Wirbel sich linksherum dreht, negative Werte, dass er sich rechtsherum dreht.
Im Inneren des Wirbels ist \(\zeta\) konstant und nimmt dann nach außen hin ab.
Wirbel sind oft über lange Zeit stabil, weil ihre Strömung geostrophisch angepasst ist. Wenn die Dichte im Wirbel anders ist als die im umgebenden Wasser, ist auch der Wasserstand höher oder niedriger. Dann bildet der Wirbel quasi einen kleinen “Wasserberg” oder ein “Wassertal”. Da die Druckgradientenkraft nach außen (oder nach innen) wirkt, verläuft die geostrophische Strömung auf der Nordhalbkugel rechtsherum (oder linksherum) um den Wirbel. Das ist genau das gleiche Prinzip wie bei Hoch- und Tiefdruckgebieten in der Atmosphäre.
Weil die Dichteunterschiede meist von unterschiedlicher Temperatur verursacht sind, nennen wir die verschiedenen Wirbel “warm-core eddies” oder “cold-core eddies”.

| warm-core eddy | cold-core eddy | |
|---|---|---|
| Temperaturprofil | Warmes Wasser im Zentrum, kälteres umgebendes Wasser | Kaltes Wasser im Zentrum, wärmeres umgebendes Wasser |
| Art des Wirbels | Antizyklonisch (im Uhrzeigersinn drehend auf der Nordhalbkugel) | Zyklonisch (gegen den Uhrzeigersinn drehend auf der Nordhalbkugel) |
| Einflussbereich | Erstreckt sich typischerweise von der Oberfläche bis mehrere hundert Meter | Erstreckt sich ebenfalls von der Oberfläche bis mehrere hundert Meter |
| Effekt auf Meeresspiegel | Erhöhter Meeresspiegel | Niedrigerer Meeresspiegel |
| Auswirkungen auf den Luft-Meer-Fluss | Erhöht im Allgemeinen den Wärmefluss vom Ozean zur Atmosphäre | Reduziert im Allgemeinen den Wärmefluss vom Ozean zur Atmosphäre |
| Lebensdauer | Kann mehrere Monate bestehen, oft 3-6 Monate oder länger | Ähnliche Lebensdauer, typischerweise ebenfalls mehrere Monate |
| Biologisch | meist nährstoffarm | meist nährstoffreich |
Cold-core Eddies entstehen meist, indem nährstoffreiches Tiefenwasser angehoben wird. Wenn sie dann in wärmere Meeresregionen wandern, können sie Nährstoffe mitbringen und dort z.B. Algenblüten auslösen.

An diesem Satellitenbild kann man zum Beispiel gut erkennen, dass wir auf der Südhalbkugel sind. Das kalte Wasser aus dem kalten und nährstoffreichen Südpolarmeer bildet hier cold-core eddies, die sich im Uhrzeigersinn drehen. Diese sind durch die Algenblüten zu erkennen. Die warm-core eddies, die auch da sind, sieht man nicht, denn sie haben kein Chlorophyll.
Wenn sich ein Wasserpaket bewegt, dann behält es nicht unbedingt seine Vorticity. Der Grund ist, dass es sich in Wahrheit ja mit anderer Geschwindigkeit dreht, weil die Erdrotation mitspielt.
Wir bezeichnen \(\zeta\) daher auch als “relative Vorticity”. Eigentlich dreht es sich ja auch noch um die Erdachse, wobei wir da nur den Anteil um die vertikale Achse (die \(z\)-Achse) betrachten. Diese Drehung erfolgt mit dem lokalen Coriolisparameter \(f\), so dass wir \(f+\zeta\) als “absolute Vorticity” bezeichnen. Solange die Wassertiefe dieselbe ist, behält ein Wasserpaket seine absolute Vorticity, also seine Winkelgeschwidigkeit.
Sehen wir uns das mal auf der Nordhalbkugel an. Ein Wasserpaket ist in Ruhe, dreht sich nicht. Nun wird es von der Strömung südwärts transportiert. Der lokale Coriolisparameter nimmt ab. Damit \(f+\zeta\) erhalten wird, fängt das Wasserpaket also an zu rotieren, es erhält ein \(\zeta>0\), dreht sich entgegen dem Uhrzeigersinn (wie die Erdrotation).
Bewegt es sich nach Norden, dann rotiert es stattdessen rechtsherum (\(\zeta<0\)).
https://www.youtube.com/watch?v=nwyd5_8eIMM
Im Allgemeinen wird aber nicht die Winkelgeschwindigkeit erhalten, sondern das Trägheitsmoment. Wenn sich die Masse eines Körpers näher an die Drehachse herangeführt wird, dreht es sich schneller. Ein Beispiel sind Pirouetten im Eiskunstlauf.
https://www.youtube.com/watch?v=AQLtcEAG9v0
So ähnlich funktioniert das auch beim Wasser, wenn es von flachen in tiefe Gebiete strömt. Betrachten wir mal einen Wasserzylinder, der im Flachwasser ist. Wenn er ins Tiefwasser gerät, verändert er nicht nur seine Tiefe, sondern entsprechend auch seinen Radius, er wird schmaler.
Der Trick ist nun, dass sich dadurch nicht die relative, sondern die absolute Vorticity ändert. Es ergibt sich eine neue Erhaltungsgröße: Die potentielle Vorticity.
\[ \frac{\mathrm{D}}{\mathrm{D}t} \frac{f+\zeta}{H+\eta} = 0 \]
Wir kennen nun vier Arten von Vorticity, wie die folgende Tabelle zeigt:
| Formel | Bezeichnung | beschreibt |
|---|---|---|
| \(\zeta\) | relative Vorticity | Drehung des Wassers um die \(z\)-Achse, relativ zur Umgebung |
| \(f\) | planetare Vorticity | Drehung der Erde um die \(z\)-Achse |
| \(f+\zeta\) | absolute Vorticity | Drehung des Wassers inkl. Erdrotation |
| \(\frac{f+\zeta}{H+\eta}\) | potentielle Vorticity | wie klein die absolute Vorticity würde, wenn man das Wasser in ein Gebiet mit nur 1 m Wassertiefe bewegt |
Machen wir ein Beispiel für die Erhaltung der potentiellen Vorticity: Ein Wasserpaket auf der Nordhalbkugel ist in Ruhe (\(\zeta=0\), \(f>0\)). Wir sehen dass der Zähler also gleich \(f\) ist. Das Wasserpaket strömt nun ostwärts in ein Gebiet doppelter Tiefe. Wir nehmen an, dass der Wasserstand bei \(\eta=0\) bleibt. Dann verdoppelt sich der Nenner, und also muss sich auch der Zähler verdoppeln. Da \(f\) natürlich konstant bleibt, muss nun \(\zeta=f\) gelten, damit der Zähler sich auch verdoppeln kann auf \(2*f\). Das Wasserpaket dreht sich also nun linksherum, in Richtung der Erdrotation und zusätzlich zu dieser.

Ein nicht rotierendes Wasserpaket kann also anfangen zu rotieren (und damit einen Eddy bilden), wenn es:
sich nord- oder südwärts bewegt, oder
sich in flacheres oder tieferes Wasser bewegt.
Das ist die Ursache dafür, dass es im Meer so viele Wirbel gibt.
Wirbel können quasi “Wirbelstraßen” bilden. Zum Beispiel, wenn sie abwechselnd nordwärts und südwärts ausgelenkt werden und entsprechend rotieren.
Diese laufen westwärts, und zwar auf der Nord- und der Südhalbkugel und heißen dann Rossbywellen.
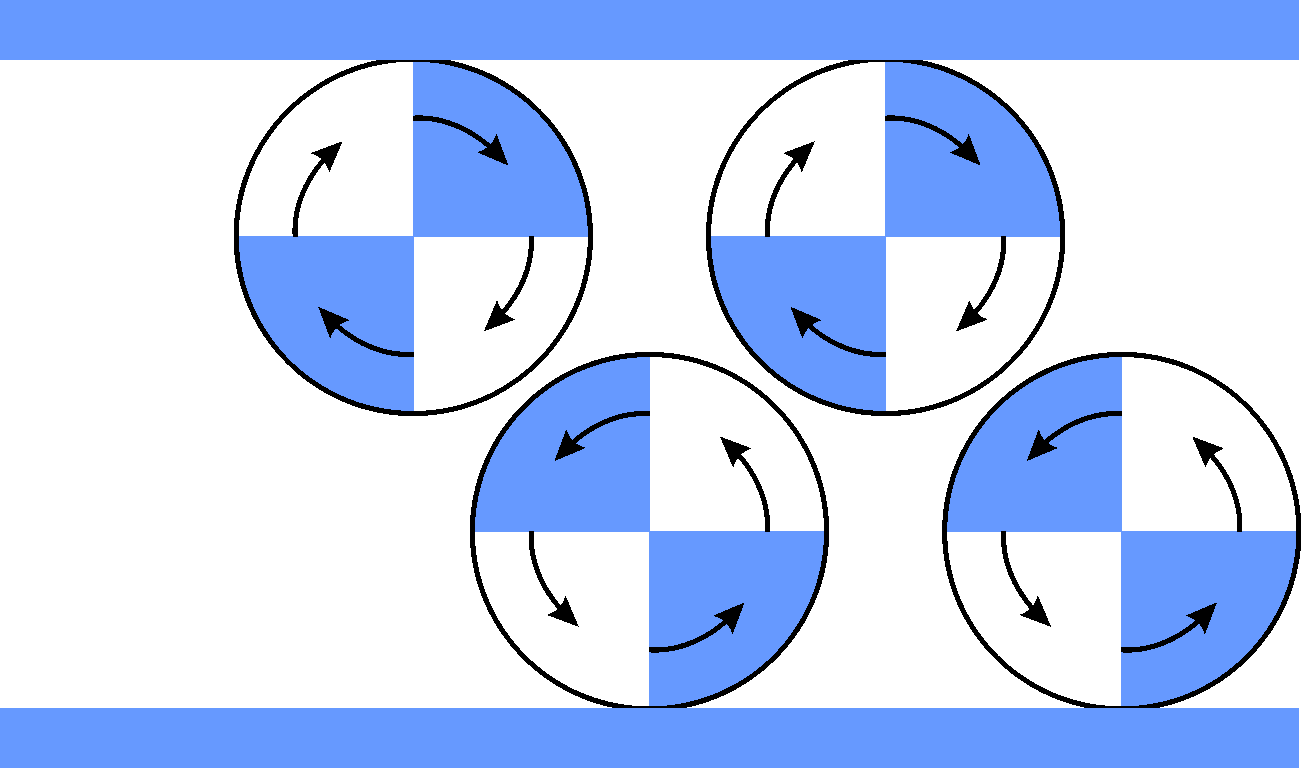
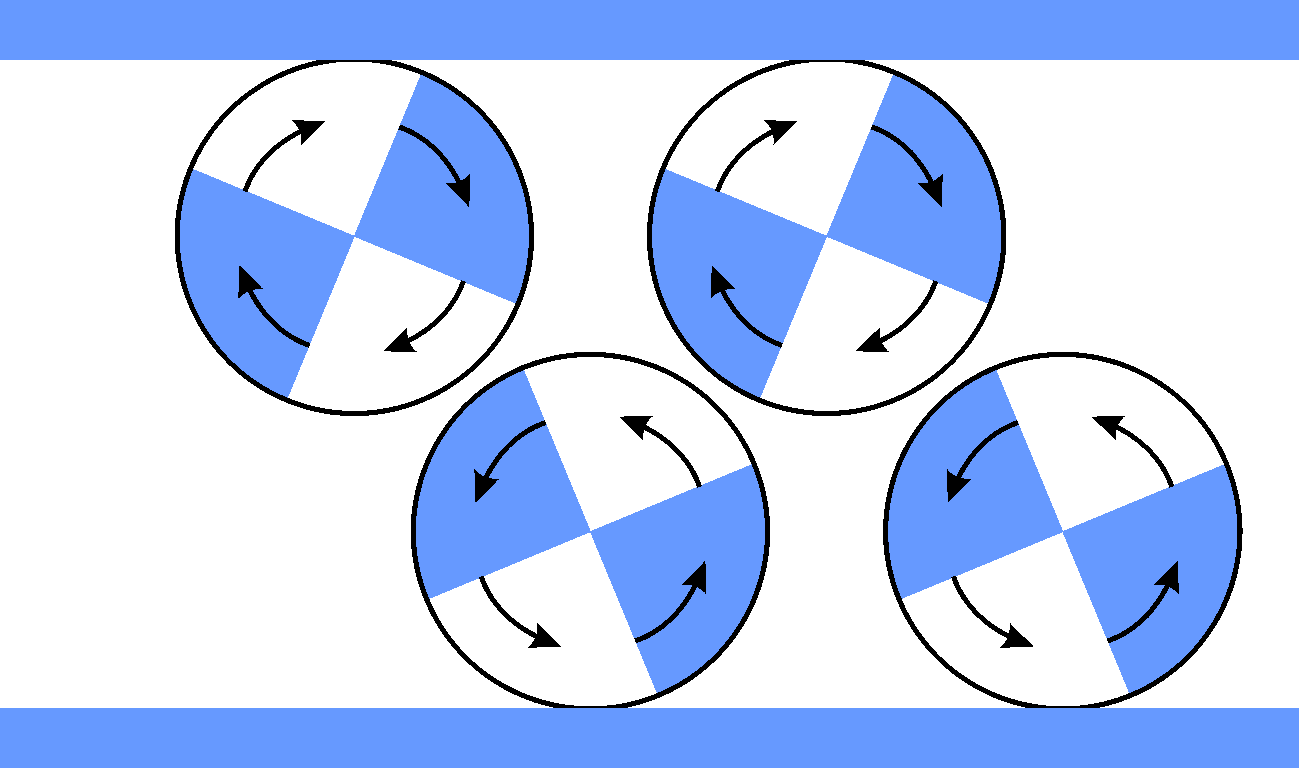
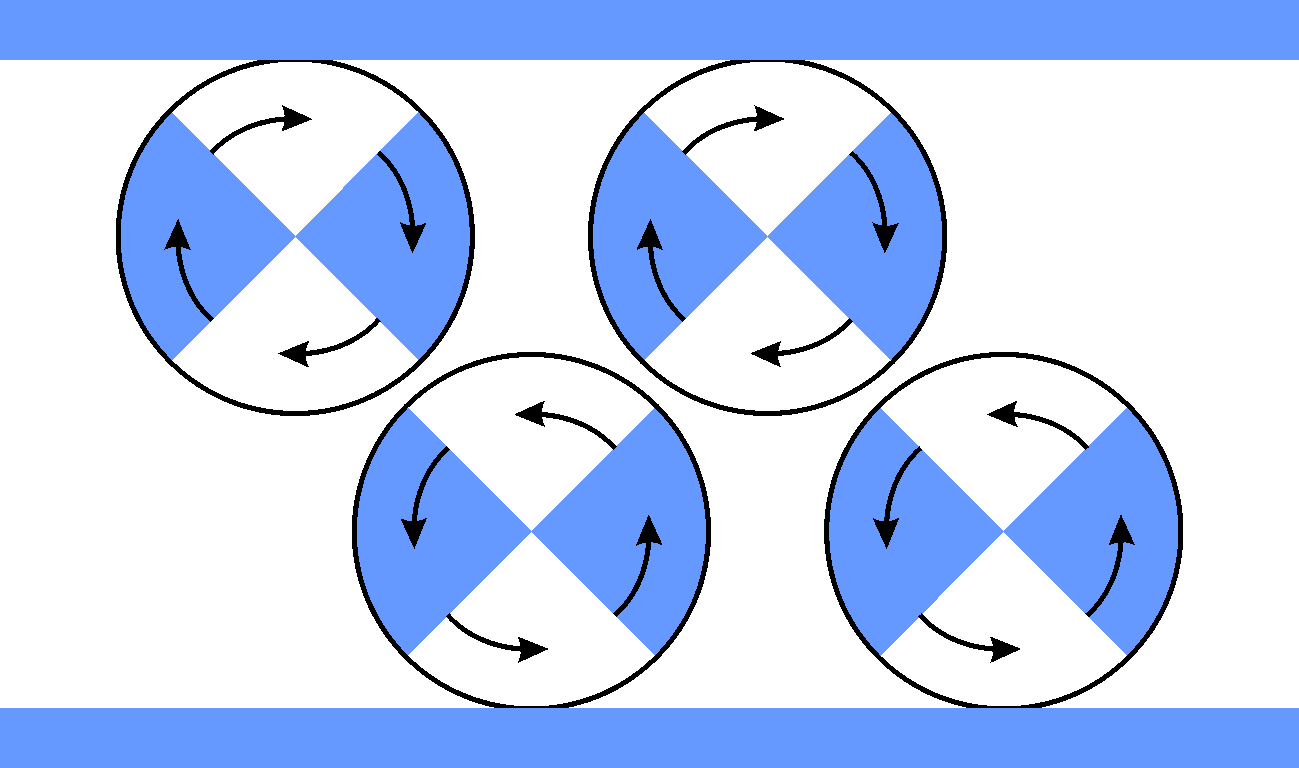
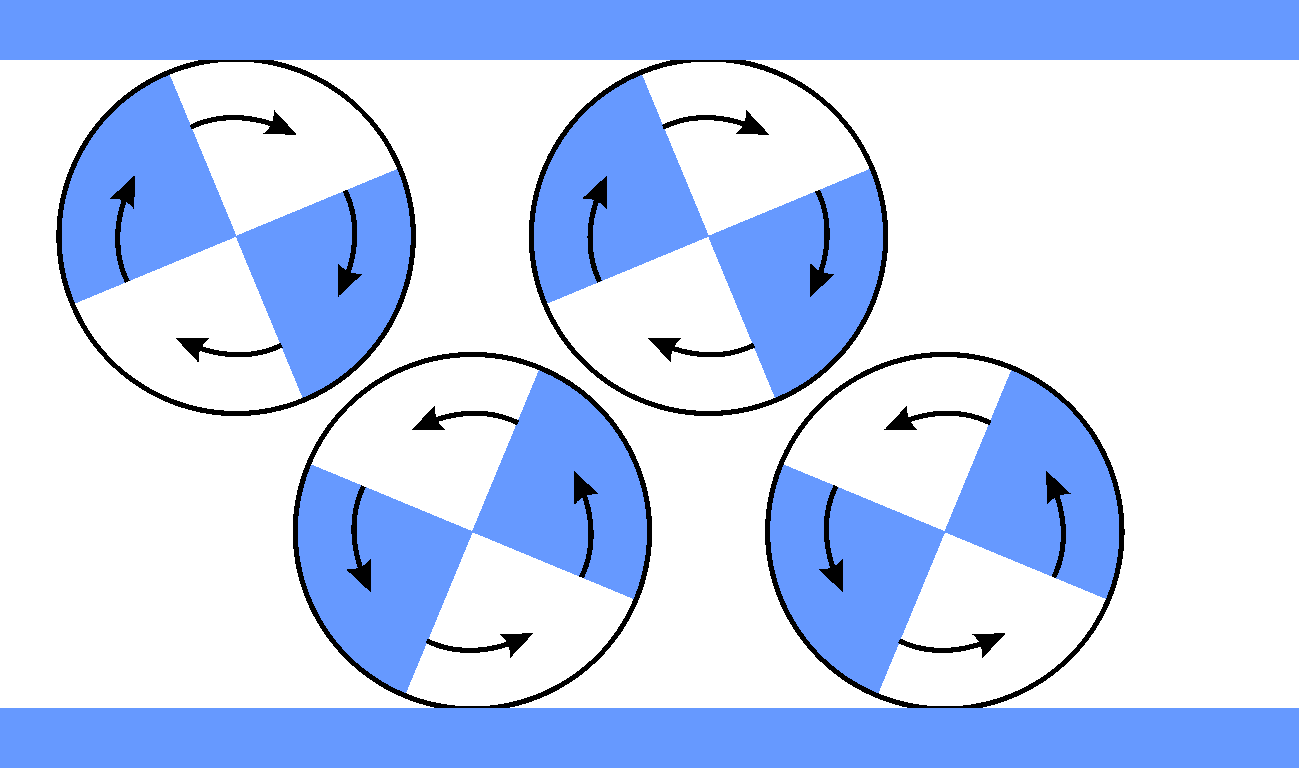
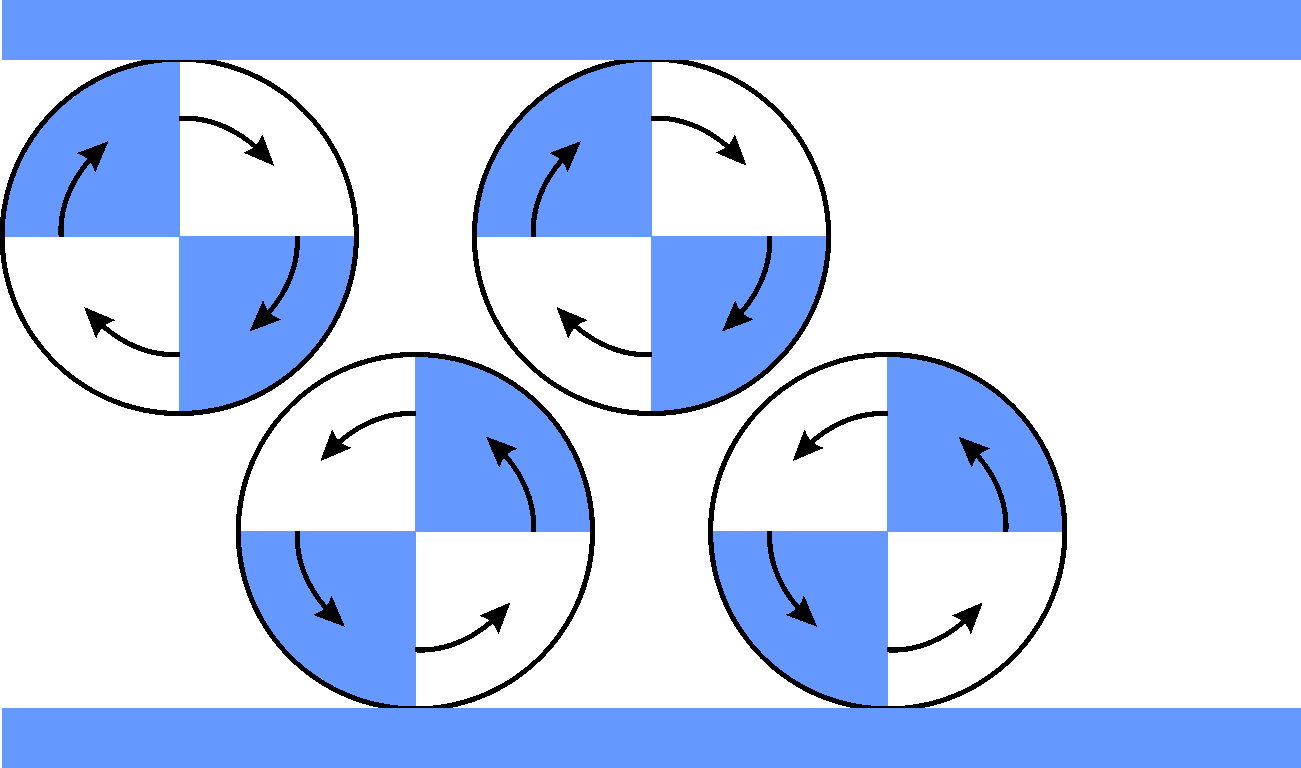
Die gibt es im Ozean und in der Atmosphäre. In der Atmosphäre verursachen sie Extremwetter, weil sie Luftmassen weit nordwärts oder weit südwärts auslenken.
Bisher haben wir uns geostrophisch angepasste Phänomene angeschaut. Das waren geostrophische Strömungen und Eddies. Dabei waren immer nur Druckgradienten und die Corioliskraft relevant.
Jetzt wollen wir Gebiete im Meer anschauen, wo der Windschub eine wichtige Rolle spielt. Dazu sehen wir uns mal wieder unsere volle Navier-Stokes-Gleichung an:
\[ \frac{\partial \vec{u}}{\partial t} = - \left( \vec{u} \cdot \vec{\nabla} \right) \vec{u} \color{blue}{\,+ \frac{1}{\rho} \cdot \begin{pmatrix} X \\ Y \\ 0 \end{pmatrix}} \color{green}{\,- g \vec{e}_z} \color{orange}{\,- \frac{1}{\rho} \vec{\nabla} \cdot p } \color{red}{\,+ \left( \nu_x \frac{\partial^2}{\partial x^2} + \nu_y \frac{\partial^2}{\partial y^2} + \nu_z \frac{\partial^2}{\partial z^2} \right) \vec{u} } \color{magenta}{\,+ \begin{pmatrix} f \cdot v \\ -f \cdot u \\ 0 \end{pmatrix}} \]
Nun sagen wir wieder in einem simplen Spezialfall, dass nur zwei Kräfte relevant sind:
Windschub
Corioliskraft
Wir können in der Gleichung wieder fast alles streichen.
\[ \cancel{\frac{\partial \vec{u}}{\partial t}} = - \cancel{\left( \vec{u} \cdot \vec{\nabla} \right) \vec{u} } \color{blue}{\,+ \frac{1}{\rho} \cdot \begin{pmatrix} X \\ Y \\ 0 \end{pmatrix}} \color{green}{\,- \cancel{g \vec{e}_z}} \color{orange}{\,- \cancel{\frac{1}{\rho} \vec{\nabla} \cdot p }} \color{red}{\,+ \cancel{\left( \nu_x \frac{\partial^2}{\partial x^2} + \nu_y \frac{\partial^2}{\partial y^2} + \nu_z \frac{\partial^2}{\partial z^2} \right) \vec{u} }} \color{magenta}{\,+ \begin{pmatrix} f \cdot v \\ -f \cdot u \\ 0 \end{pmatrix}} \]
Wir erhalten also wieder zwei recht einfache Gleichungen (in \(x\)- und \(y\)-Richtung), mit der wir die Strömung ausrechnen können:
\[ 0 = \frac{X}{\rho} + f v \]
\[ 0 = \frac{Y}{\rho} - f u \]
Es ergibt sich als Strömung:
\[ u = \frac{Y}{f \rho} \]
\[ v = - \frac{X}{f \rho} \]
Wie wir sehen, ist die Strömung gerade nicht in Windrichtung gerichtet. Sie verläuft auf der Nordhalbkugel 90° rechts zum Wind, auf der Südhalbkugel 90° links zum Wind. Dieser Effekt wird als Ekman-Transport bezeichnet.
Er findet überall auf der Erde statt, außer um den Äquator herum, weil dort keine (horizontale) Corioliskraft wirkt.
Seine Bedeutung liegt vor allem darin, dass er durch verschiedene Mechanismen zu Auftrieb von Tiefenwasser führt, indem er eine horizontale Divergenz verursacht. Wenn man auf das Chlorophyll schaut, sieht man, dass die Meeresgebiete sehr unterschiedlich produktiv sind:

Das liegt daran, dass nährstoffreiches Tiefenwasser an die Oberfläche transportiert wird. Die wichtigsten Mechanismen wollen wir uns hier ansehen.
Der bekannteste Mechanismus ist der Küstenauftrieb (coastal upwelling).
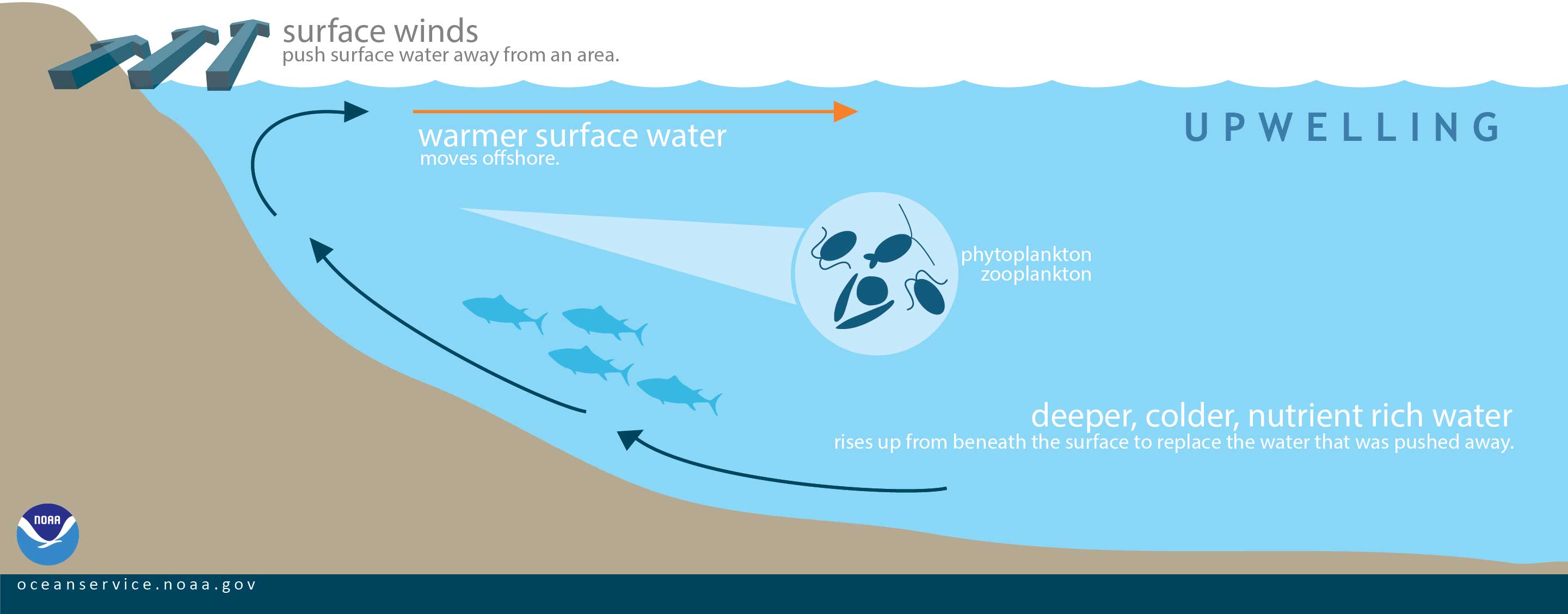
Der Wind weht parallel zur Küste. Der Ekman-Transport ist von der Küste weg gerichtet. Weil von Land her kein Wasser nachströmen kann, entsteht eine horizontale Divergenz. Die Volumenerhaltung bewirkt, dass Tiefenwasser nach oben befördert wird.
Das Oberflächenwasser im Meer ist im Gegensatz zum Tiefenwasser typischerweise nährstoffarm, so dass ohne diese Nährstoffzufuhr nur wenig Primärproduktion möglich ist. Der Grund ist, dass die Bildung von Organismen die gelösten Stoffe zu Partikeln macht. So wird durch Primärproduktion zumeist
gelöster anorganischer Kohlenstoff (DIC) zu partikulärem organischen Kohlenstoff (POC),
gelöster anorganischer Stickstoff (DIN) zu partikulärem organischen Stickstoff (PON), und
gelöster anorganischer Phosphor (DIP) zu partikulärem organischen Phosphor (POP).
Die Partikel sinken irgendwann ab. Dies wird (in Bezug auf den Kohlenstoff) auch als “biological carbon pump” bezeichnet. Das ist wichtig, weil es den Klimawandel hinauszögert. Und zwar in der Größenordnung 1 Jahrhundert bis wenige Jahrhunderte, denn so lange dauert es (je nach Ort im Meer), bis das Tiefenwasser wieder an die Oberfläche kommt und das CO2 wieder frei wird.
Küstenauftrieb kann man auch auf Satellitenbildern der Meeresoberflächentemperatur sehen:
Wichtige Gebiete für Küstenauftrieb sind Benguela (vor Namibia), die chilenische und die kalifornische Küste, wie man in dieser Visualisierung schön erkennen kann:
https://svs.gsfc.nasa.gov/30008
Das sind dann auch jeweils beliebte Fischfanggebiete, weil die starke Primärproduktion ein komplexes Nahrungsnetz begründet.
Den umgekehrten Effekt gibt es auch, wenn der Ekman-Transport zur Küste hin gerichtet ist: Downwelling.
Auch unter Tiefdruckgebieten kann es dazu kommen, dass Tiefenwasser an die Oberfläche “gesaugt” wird. Auf der Nordhalbkugel rotieren diese linksherum. Das bedeutet, dass der Ekman-Transport (90° rechts zum Wind) nach außen gerichtet ist. In der Mitte haben wir also eine horizontale Divergenz, und die führt zu Auftrieb.
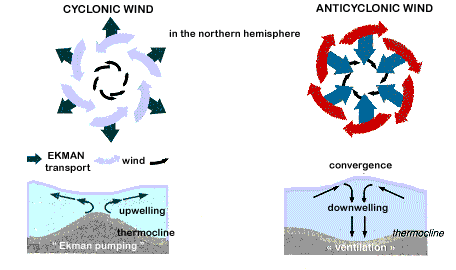
Umgekehrt verhält es sich bei Hochdruckgebieten. Hier ist der Ekman-Transport nach innen gerichtet und es kommt zu Downwelling. Damit kennen wir nun auch der Grund, dass sich die Müllteppiche im subtropischen Hochdruckgürtel bilden. Das liegt an der horizontalen Konvergenz des Ekman-Transports.
Tatsächlich wird oft für Küstenauftrieb gehalten, was in Wahrheit “Ekman Pumping” ist. Der Grund ist, dass der küstenparallele Wind oft in Richtung Land schwächer wird. Damit entsteht die Divergenz im Ekman-Transport nur in Küstennähe, aber nicht direkt an der Küste.
Ein weiterer Mechanismus ist der äquatoriale Auftrieb. Die Passatwinde kommen auf der Nordhalbkugel aus Nordost, der Ekman-Transport wird 90° nach rechts abgelenkt. Auf der Südhalbkugel kommen sie aus Südost, der Ekman-Transport wird 90° nach links abgelenkt. Direkt am Äquator gibt es keinen Ekman-Transport.
Der Ekman-Transport geht auf der Nordhalbkugel also nach Nordwest, auf der Südhalbkugel nach Südwest. Das bewirkt eine Divergenz. Wieder wird Tiefenwasser hochgepumpt.
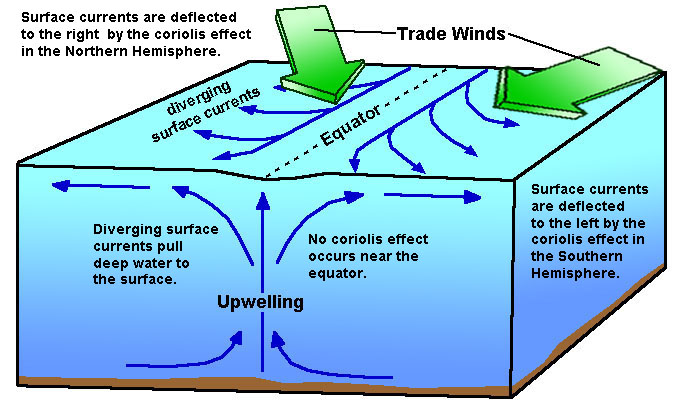
Eines der produktivsten Meeresgebiete ist die Antarktis. Hier treffen Westwindgürtel und polare Ostwinde aufeinander. Wieder strömt der Ekman-Transport auseinander, und es kommt zu Auftrieb.

Allerdings wird ein teil des schweren salzhaltigen Wassers auch in die Zone der Eisbildung transportiert. Die katabatischen Winde (kalte Fallwinde) kühlen das Wasser extrem ab. Es wird noch kälter und noch salziger. Deshalb wird in der Antarktis das schwerste Wasser auf der Welt produziert.
Ein schönes Beispiel für andere katabatische Winde sieht man hier: https://www.youtube.com/watch?v=B2lpFhB_cqE
Wenn wir wieder auf die Chlorophyll-Karte schauen, können wir uns nun die meisten hellgrünen Flecken erklären. Die hohen Konzentrationen in Küstennähe kommen oft einfach von Nährstoffen aus Flusseinträgen.

In der nächsten Vorlesung werden wir uns mit “Jets” befassen, also mit windgetriebenen Strömungen, die in Windrichtung verlaufen, und schauen, wo die vorkommen können.