<– Zurück zur Übersicht

Rotierende Erde

Vier Kräfte haben wir in der letzten Vorlesung kennengelernt, die auf das Meerwasser wirken:

• Windschubkraft

• Gewichtskraft

• Druckgradientenkraft

• Reibungskraft

Eine fünfte “Kraft” ist von entscheidender Bedeutung für das Verständnis der Meeresströmungen. Die Corioliskraft ist keine echte Kraft, sondern eine Scheinkraft, die aufgrund der Rotation der Erde um ihre eigene Achse entsteht.

Betrachten wir zunächst mal die Erde. Sie dreht sich um ihre Achse von West nach Ost, also, wenn man auf den Nordpol schaut, entgegen dem Uhrzeigersinn. Darum wandert die Sonne scheinbar von Ost nach West.

Die Dauer einer Umdrehung ist nicht etwa 24 h. Das wäre ein Sonnentag: Von einem Höchststand der Sonne bis zum nächsten. Ein Sterntag ist nur 23 Stunden 56 Minuten 4 Sekunden lang, denn davon gibt es im Jahr genau einen mehr. Die Sonne läuft scheinbar langsamer über den Himmel als die Sterne, weil die Erde ja gleichzeitig zu ihrer eigenen Rotation auch noch um die Sonne umläuft. Damit geht ein Sonnentag pro Jahr verloren.

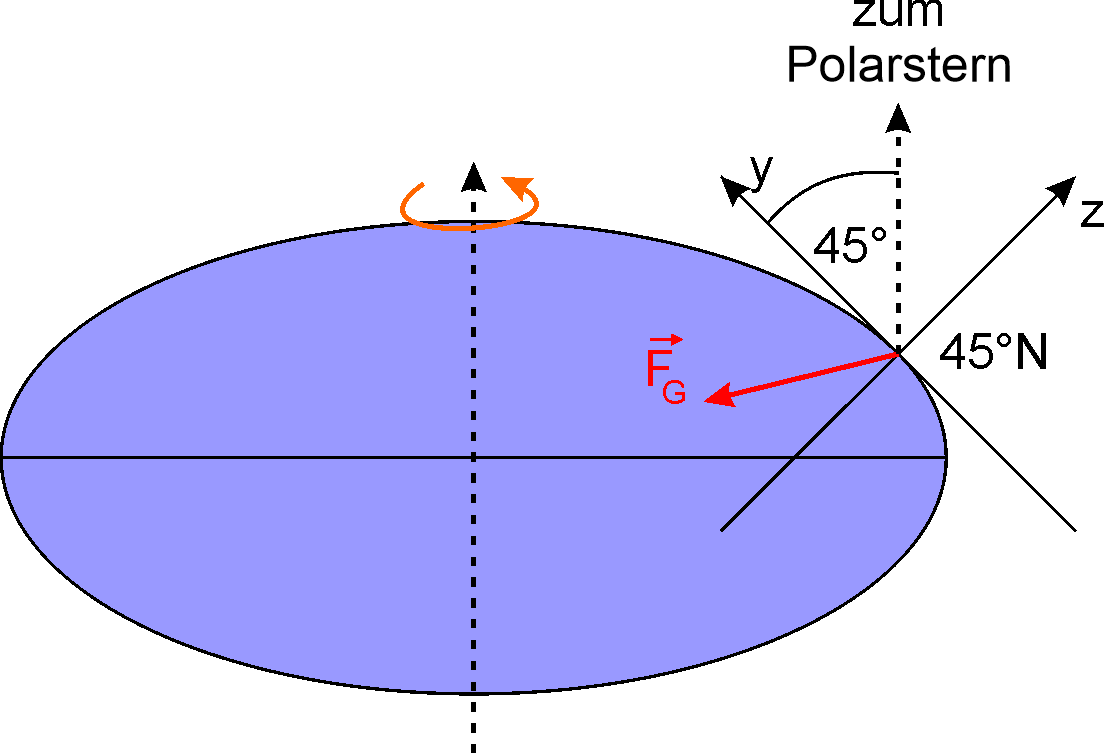
Die Erde ist keine Kugel. Sie hat annähernd die Form eines Rotationsellipsoids ($\approx$ gestauchte Kugel), der Abstand zum Erdmittelpunkt ist am Äquator größer als am Pol. Stellen wir das mal übertrieben dar, sieht man, dass die Breitenkreise nicht gleich weit voneinander entfernt sind. Entscheidend ist, wie hoch der Polarstern (der in Richtung der Erdachse liegt) über dem Horizont steht.

Ebenso hat das zur Folge, dass die $z$-Achse, die senkrecht auf der Meeresoberfläche steht, in der Regel nicht durch den Erdmittelpunkt verläuft. Zu dem hin wirkt ja aber die Schwerkraft, das ist also etwas verwirrend warum das Wasser “schief steht”.

Die elliptische Form der Erde, hier übertrieben dargestellt.

Das liegt an sogenannten “Scheinkräften”, die wir uns jetzt ansehen wollen.

Die Newtonschen Axiome gelten nur in einem Inertialsystem, d.h. das Koordinatensystem ist selbst in Ruhe oder bewegt sich gleichförmig in eine Richtung. Das ist für unser Koordinatensystem $x$, $y$, $z$ natürlich nicht so, denn das dreht sich ja mit der Erde mit.

Die Drehung können wir beschreiben durch einen Rotationsvektor. Der verläuft entlang der Drehachse, und sein Betrag ist

$$\omega =|\overrightarrow{\omega }|=\frac{2\pi }{T}$$

wobei $T$ die Zeit für eine volle Umdrehung ist, in unserem Fall der Sterntag (23,93 h).

Dann treten zwei Scheinkräfte auf:

• Fliehkraft: ${\overrightarrow{F}}_z=m{\omega }^2\overrightarrow{r}$ (Hierbei ist $\overrightarrow{r}$ der Vektor, der von der Drehachse zum Körper zeigt.)

• Corioliskraft: ${\overrightarrow{F}}_c=-2m\overrightarrow{\omega }\times \overrightarrow{u}$

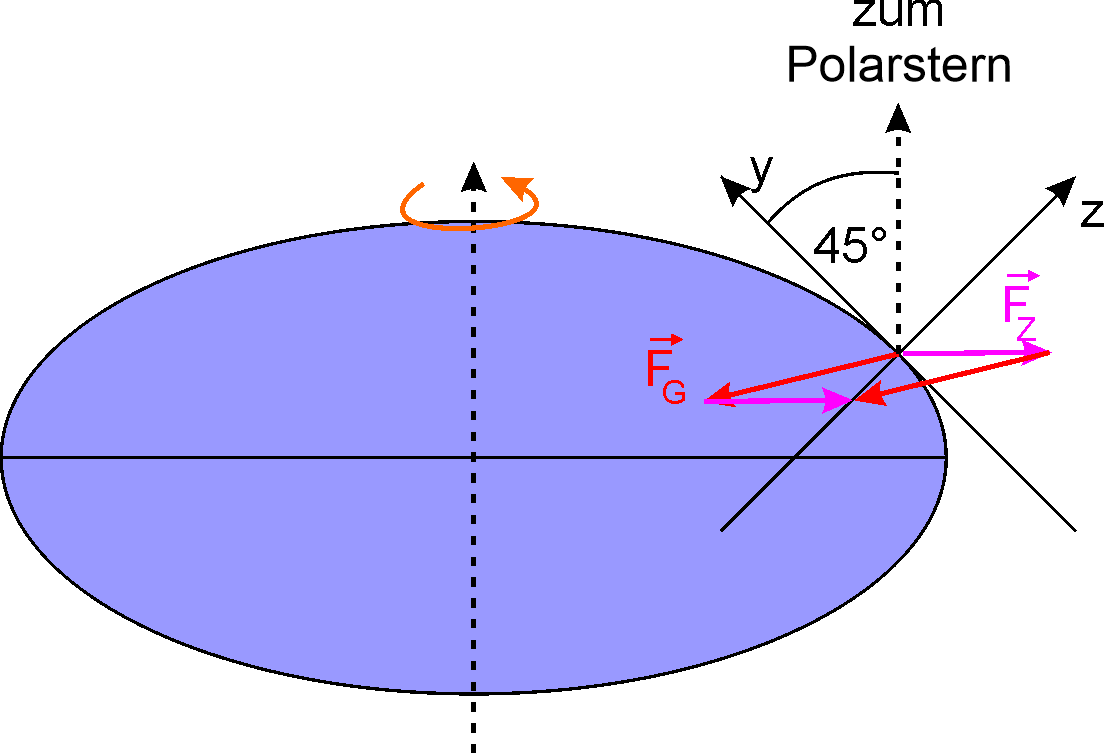
Die Fliehkraft oder Zentrifugalkraft werden wir nicht groß weiter behandeln. Ihr einziger relevanter Effekt ist, dass sie die Erde zum Ellipsoid macht. Die Fliehkraft wirkt nach außen. Das kompensiert den Umstand, dass die Schwerkraft auf dem Ellipsoid teilweise nach innen wirkt. In der Summe ergibt sich eine Kraft entlang der $z$-Achse nach unten, siehe nächste Grafik:

Die Fliehkraft als Scheinkraft bewirkt, dass die Gravitation scheinbar nach unten gerichtet ist, und nicht schief zum Erdmittelpunkt hin.

Die Corioliskraft hingegen ist sehr wichtig für die Ozeanographie und schwieriger zu verstehen. In ihrer Formel taucht das Kreuzprodukt auf, das wollen wir erstmal wiederholen.

Auffrischung: Kreuzprodukt

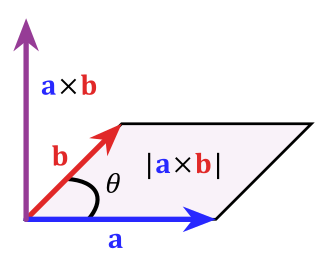
Das Kreuzprodukt $\overrightarrow{a}\times \overrightarrow{b}$ zweier Vektoren ist wieder ein Vektor. Er hat folgende Eigenschaften:

• Er steht senkrecht auf beiden Vektoren.

• Die Vektoren $\overrightarrow{a}$, $\overrightarrow{b}$ und $\overrightarrow{a}\times \overrightarrow{b}$ bilden dabei ein Rechtssystem.

• Seine Länge entspricht dem Flächeninhalt des von $\overrightarrow{a}$ und $\overrightarrow{b}$ aufgespannten Parallelogramms.

Das Kreuzprodukt.
[https://upload.wikimedia.org/wikipedia/commons/thumb/4/4e/Cross_product_parallelogram.svg/330px-Cross_product_parallelogram.svg.png]

Wie wird es berechnet? Über Kreuz. Wir machen ein Beispiel.

$$\overrightarrow{a}=\left(\begin{array}{c}1\\ 2\\ 5\end{array}\right),\overrightarrow{b}=\left(\begin{array}{c}3\\ 1\\ 2\end{array}\right)$$

Zunächst verlängern wir die Vektoren, indem wir unten die ersten beiden Einträge wiederholen:

$$\left(\begin{array}{c}1\\ 2\\ 5\\ 1\\ 2\end{array}\right)\left(\begin{array}{c}3\\ 1\\ 2\\ 3\\ 1\end{array}\right)$$

Jetzt streichen wir die erste Zeile und rechnen in den beiden Zeilen darunter schräg runter minus schräg rauf. Das wird das erste Element des neuen Vektors:

$$\left(\begin{array}{c}\cancel{1}\\ 2\\ 5\\ 1\\ 2\end{array}\right)\left(\begin{array}{c}\cancel{3}\\ 1\\ 2\\ 3\\ 1\end{array}\right)\to \left(\begin{array}{c}2\cdot 2-5\cdot 1\\ \\ \end{array}\right)=\left(\begin{array}{c}-1\\ \\ \end{array}\right)$$

Wir streichen die zweite Zeile und rechnen wieder schräg runter minus schräg rauf:

$$\left(\begin{array}{c}\cancel{1}\\ \cancel{2}\\ 5\\ 1\\ 2\end{array}\right)\left(\begin{array}{c}\cancel{3}\\ \cancel{1}\\ 2\\ 3\\ 1\end{array}\right)\to \left(\begin{array}{c}2\cdot 2-5\cdot 1\\ 5\cdot 3-1\cdot 2\\ \end{array}\right)=\left(\begin{array}{c}-1\\ 13\\ \end{array}\right)$$

Wir streichen die dritte Zeile und erhalten das dritte und letzte Element:

$$\left(\begin{array}{c}\cancel{1}\\ \cancel{2}\\ \cancel{5}\\ 1\\ 2\end{array}\right)\left(\begin{array}{c}\cancel{3}\\ \cancel{1}\\ \cancel{2}\\ 3\\ 1\end{array}\right)\to \left(\begin{array}{c}2\cdot 2-5\cdot 1\\ 5\cdot 3-1\cdot 2\\ 1\cdot 1-2\cdot 3\end{array}\right)=\left(\begin{array}{c}-1\\ 13\\ -5\end{array}\right)$$

Corioliskraft

Nun können wir die Corioliskraft ausrechnen. Allerdings wollen wir wohl eher die Corioliskraftdichte ausrechnen, denn wir rechnen ja immer mit Kraftdichten.

Berechnung der Corioliskraftdichte

Wir verwenden also die Dichte $\rho$ statt der Masse $m$ in der Formel:

$${\overrightarrow{F}}_c=-2\rho \overrightarrow{\omega }\times \overrightarrow{u}$$

Den Betrag des Rotationsvektors $\overrightarrow{\omega }$ kennen wir ja schon, das ist

$$\omega =|\overrightarrow{\omega }|=\frac{2\pi }{23.93\mathrm{h}}=7.29\cdot {10}^{-5}{\mathrm{s}}^{-1}=0.0000729{\mathrm{s}}^{-1}$$

Aber wir brauchen auch seine Richtung, und zwar in unserem mitrotierenden Koordinatensystem.

Die können wir aus folgender Grafik entnehmen:

Der Rotationsvektor $\overrightarrow{\omega }$ im lokalen, mitrotierenden Koordinatensystem.

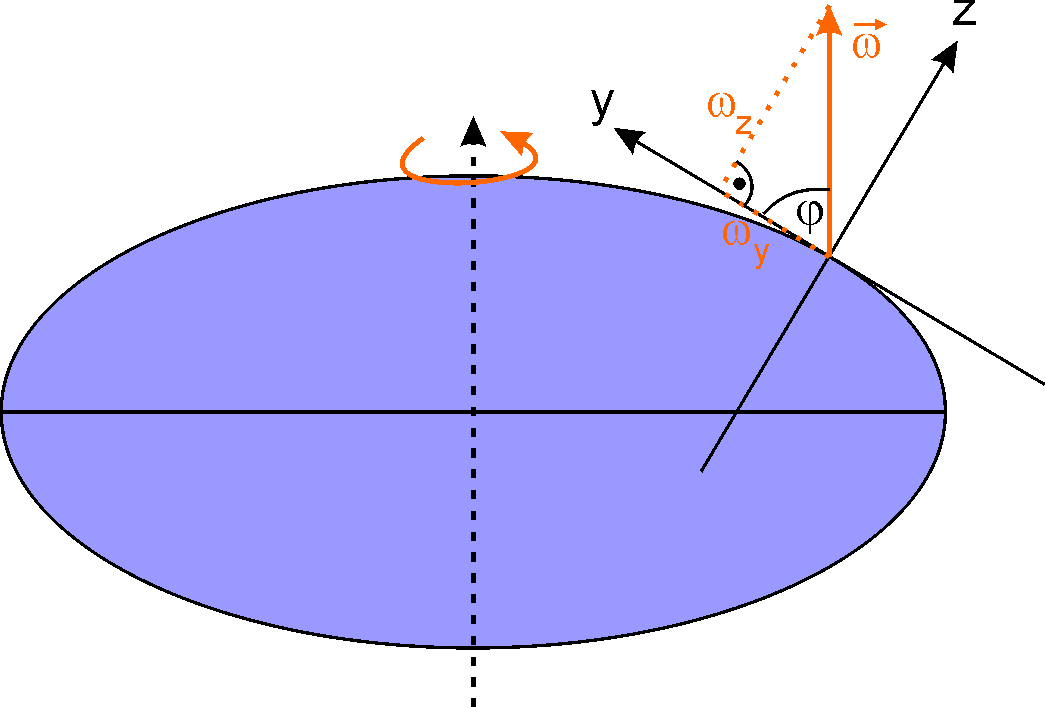
Der Vektor $\overrightarrow{\omega }$ verläuft parallel zur Drehachse, der Erdachse. Damit ist er (auf der Nordhalbkugel) teilweise nordwärts und teilweise aufwärts gerichtet. Da das orange Dreieck in obiger Abbildung rechtwinklig ist, ergeben sich die entsprechenden Komponenten aus dem Breitengrad $\phi$:

$${\omega }_y=\omega \cdot \cos (\phi )$$

$${\omega }_z=\omega \cdot \sin (\phi )$$

Und wir erhalten als Vektor

$$\overrightarrow{\omega }=\left(\begin{array}{c}0\\ \omega \cos (\phi )\\ \omega \sin (\phi )\end{array}\right)$$

Damit können wir die Corioliskraftdichte ausrechnen:

$${\overrightarrow{F}}_c=-2\rho \left(\begin{array}{c}0\\ \omega \cos (\phi )\\ \omega \sin (\phi )\end{array}\right)\times \left(\begin{array}{c}u\\ v\\ w\end{array}\right)$$

Bevor wir das tun, machen wir eine Näherung (denn der Physiker liebt Näherungen): Die vertikale Geschwindigkeit ist viel kleiner als die horizontale, also vernachlässigen wir sie. Wir erhalten dann:

$${\overrightarrow{F}}_c\approx -2\rho \left(\begin{array}{c}0\\ \omega \cos (\phi )\\ \omega \sin (\phi )\end{array}\right)\times \left(\begin{array}{c}u\\ v\\ 0\end{array}\right)$$

$${\overrightarrow{F}}_c\approx -2\rho \left(\begin{array}{c}-\omega \sin (\phi )\cdot v\\ \omega \sin (\phi )\cdot u\\ -\omega \cos (\phi )\cdot u\end{array}\right)$$

Noch eine Näherung: Die vertikale Komponente der Corioliskraft ist viel kleiner als die anderen vertikalen Kräfte wie die Gewichtskraft, darum setzen wir sie auch auf null.

$${\overrightarrow{F}}_c\approx \rho \left(\begin{array}{c}2\omega \sin (\phi )\cdot v\\ -2\omega \sin (\phi )\cdot u\\ 0\end{array}\right)$$

Das ist doch nett. Wir haben nur noch 2 Komponenten.

Wir definieren nun noch eine Abkürzung:

$$f=2\omega \sin (\phi )$$

wir der lokale Coriolisparameter genannt. Für unseren Breitengrad (54°N) ergibt sich z.B.

$$f({54}^{\circ }\mathrm{N})=1.18\cdot {10}^{-4}{\mathrm{s}}^{-1}=0.000118{\mathrm{s}}^{-1}$$

Damit lässt sich die Corioliskraft sehr einfach schreiben:

$${\overrightarrow{F}}_c\approx \rho \left(\begin{array}{c}f\cdot v\\ -f\cdot u\\ 0\end{array}\right)$$

Wir sehen, dass auf der Nordhalbkugel ($f>0$) diese Scheinkraft immer rechts zur Strömung gerichtet ist, auf der Südhalbkugel ($f<0$) immer links zur Strömung. Am Äquator gibt es (zumindest nach unseren Näherungen) keine Corioliskraft.

Wenn wir die Dichte $\rho$ in der Formel weglassen, erhalten wir die Coriolisbeschleunigung ${\overrightarrow{a}}_c$. Die gilt für infinitesimal kleine Wasserpakete und für endliche Körper mit einer Masse $m$ gleichermaßen.

Beispiel: ICE

Ein ICE 3 mit einer Masse von 500 t fährt von Stuttgart nach Hamburg. Am 50. Breitengrad (nahe Frankfurt am Main) hat er eine Geschwindigkeit von 330 km/h und fährt genau in nordwärtiger Richtung. Wie groß ist die Corioliskraft, die seitlich auf das Gleis wirkt?

Zunächst berechnen wir den lokalen Coriolisparameter $f$:

$$f=2\omega \sin ({50}^{\circ })=1.12\cdot {10}^{-4}{\mathrm{s}}^{-1}$$

Wir rechnen in SI-Basiseinheiten um:

$$v=330\frac{\mathrm{km}}{\mathrm{h}}=91.67\frac{\mathrm{m}}{\mathrm{s}}$$

$$m=500\mathrm{t}=500000\mathrm{kg}$$

Wir berechnen zunächst die Coriolisbeschleunigung:

$${\overrightarrow{a}}_c\approx \left(\begin{array}{c}f\cdot v\\ -f\cdot u\\ 0\end{array}\right)=\left(\begin{array}{c}f\cdot v\\ 0\\ 0\end{array}\right)$$

$${\overrightarrow{a}}_c\approx \left(\begin{array}{c}1.12\cdot {10}^{-4}{\mathrm{s}}^{-1}\cdot 91.67\frac{\mathrm{m}}{\mathrm{s}}\\ 0\\ 0\end{array}\right)=\left(\begin{array}{c}0.0103\frac{\mathrm{m}}{{\mathrm{s}}^2}\\ 0\\ 0\end{array}\right)$$

Das multiplizieren wir mit der Masse und erhalten

$${\overrightarrow{F}}_c\approx \left(\begin{array}{c}500000\mathrm{kg}\cdot 0.0103\frac{\mathrm{m}}{{\mathrm{s}}^2}\\ 0\\ 0\end{array}\right)=\left(\begin{array}{c}5133\mathrm{N}\\ 0\\ 0\end{array}\right)$$

Gut 5000 Newton wirken also in östlicher Richtung auf das Gleis, was einem Gewicht von gut 500 Kilogramm entspricht.

Navier-Stokes-Gleichungen

Jetzt haben wir alle wichtigen Kräfte beisammen und können sie in die Gleichung für die lokale Änderung der Geschwindigkeit einsetzen. Die Gleichung lautete:

$$\frac{\partial \overrightarrow{u}}{\partial t}=-(\overrightarrow{u}\cdot \overrightarrow{\mathrm{\nabla }})\overrightarrow{u}+\frac{1}{\rho }\cdot \overrightarrow{F}$$

Wir erhalten dann:

$$\frac{\partial \overrightarrow{u}}{\partial t}=-(\overrightarrow{u}\cdot \overrightarrow{\mathrm{\nabla }})\overrightarrow{u}+\frac{1}{\rho }\cdot {\overrightarrow{F}}_w+\frac{1}{\rho }\cdot {\overrightarrow{F}}_g+\frac{1}{\rho }\cdot {\overrightarrow{F}}_p+\frac{1}{\rho }\cdot {\overrightarrow{F}}_r+\frac{1}{\rho }\cdot {\overrightarrow{F}}_c$$

$$\frac{\partial \overrightarrow{u}}{\partial t}=-(\overrightarrow{u}\cdot \overrightarrow{\mathrm{\nabla }})\overrightarrow{u}+\frac{1}{\rho }\cdot \left(\begin{array}{c}X\\ Y\\ 0\end{array}\right)-g{\overrightarrow{e}}_z-\frac{1}{\rho }\overrightarrow{\mathrm{\nabla }}\cdot p+({\nu }_x\frac{{\partial }^2}{\partial x^2}+{\nu }_y\frac{{\partial }^2}{\partial y^2}+{\nu }_z\frac{{\partial }^2}{\partial z^2})\overrightarrow{u}+\left(\begin{array}{c}f\cdot v\\ -f\cdot u\\ 0\end{array}\right)$$

Diese Gleichung, so oder so ähnlich, wird als Navier-Stokes-Gleichung bezeichnet. Essentiell ist, dass sie einen Advektionsterm und einen Reibungsterm enthält. Die Gleichung lässt sich mathematisch nicht exakt lösen, sondern immer nur näherungsweise.

In der Vorlesung werden wir nun Spezialfälle betrachten. Wir schauen uns Meeresgebiete oder Situationen an, wo nur wenige dieser auftretenden Kräfte groß sind und alle anderen vernachlässigbar klein. Dann kann man fast alle der Terme weglassen, und es ergibt sich eine einfache Strömung, von der man dann verstehen kann, warum sie da auftritt, wo sie auftritt.

Geostrophie

Der erste Spezialfall ist die Geostrophie. Geostrophie bedeutet, dass zwei Kräfte im Gleichgewicht sind:

• horizontale Druckgradientenkraft

• Corioliskraft

Dann ergibt sich eine stationäre Strömung die durch das Druckfeld gegeben ist.

Wir können in unserer Monstergleichung eigentlich fast alles streichen.

$$\cancel{\frac{\partial \overrightarrow{u}}{\partial t}}=-\cancel{(\overrightarrow{u}\cdot \overrightarrow{\mathrm{\nabla }})\overrightarrow{u}}+\cancel{\frac{1}{\rho }\cdot \left(\begin{array}{c}X\\ Y\\ 0\end{array}\right)}-\cancel{g{\overrightarrow{e}}_z}-\frac{1}{\rho }{\overrightarrow{\mathrm{\nabla }}}_h\cdot p+\cancel{({\nu }_x\frac{{\partial }^2}{\partial x^2}+{\nu }_y\frac{{\partial }^2}{\partial y^2}+{\nu }_z\frac{{\partial }^2}{\partial z^2})\overrightarrow{u}}+\left(\begin{array}{c}f\cdot v\\ -f\cdot u\\ 0\end{array}\right)$$

Das ${\overrightarrow{\mathrm{\nabla }}}_h$ bedeutet, dass wir vom Druckgradienten nur die horizontalen Komponenten anschauen.

Dann vereinfacht sich die Formel zu

$$\frac{1}{\rho }\frac{\partial p}{\partial x}=f\cdot v$$ $$\frac{1}{\rho }\frac{\partial p}{\partial y}=-f\cdot u$$

Oder wir können auch direkt die Strömung ausrechnen, indem wir durch $f$ teilen:

$$\frac{1}{f\cdot \rho }\frac{\partial p}{\partial x}=v$$ $$\frac{-1}{f\cdot \rho }\frac{\partial p}{\partial y}=u$$

Das bedeutet, dass die Strömung nicht, wie man vermutet, vom hohen zum niedrigen Druck strömt, sondern entlang der Isobaren (Linien gleichen Drucks).

An der Meeresoberfläche ist der Druckgradient im Wesentlichen durch Unterschiede im Wasserstand bestimmt. Den Wasserstand kann man mittlerweile mit Satelliten messen (Radaraltimetrie). Wir betrachten den Wasserstand über dem Geoid. Das ist die Form, die der Meeresspiegel hätte, wenn es keine Strömungen und keinen Wind gäbe und die Dichte des Meeres konstant wäre. Dann würden Schwerkraft und Fliehkraft überall exakt senkrecht zur Meeresoberfläche sein. Wegen verschiedener Dichte von Gesteinen weicht das ein wenig von der Ellipsoid-Form ab.

Der Geoid (die Fläche, auf der Schwerkraft plus Fliehkraft immer senkrecht stehen). Hier übertrieben dargestellt.
[https://ars.els-cdn.com/content/image/3-s2.0-B9780080449104000286-gr1.jpg]

Über diesem Geoid kann man dann wiederum den tatsächlichen Meeresspiegel messen.

Die mittlere Meeresspiegelhöhe über dem Geoid, 1993-2012, aus Satellitenmessungen.
[https://data.marine.copernicus.eu/product/SEALEVEL_GLO_PHY_MDT_008_063/description]

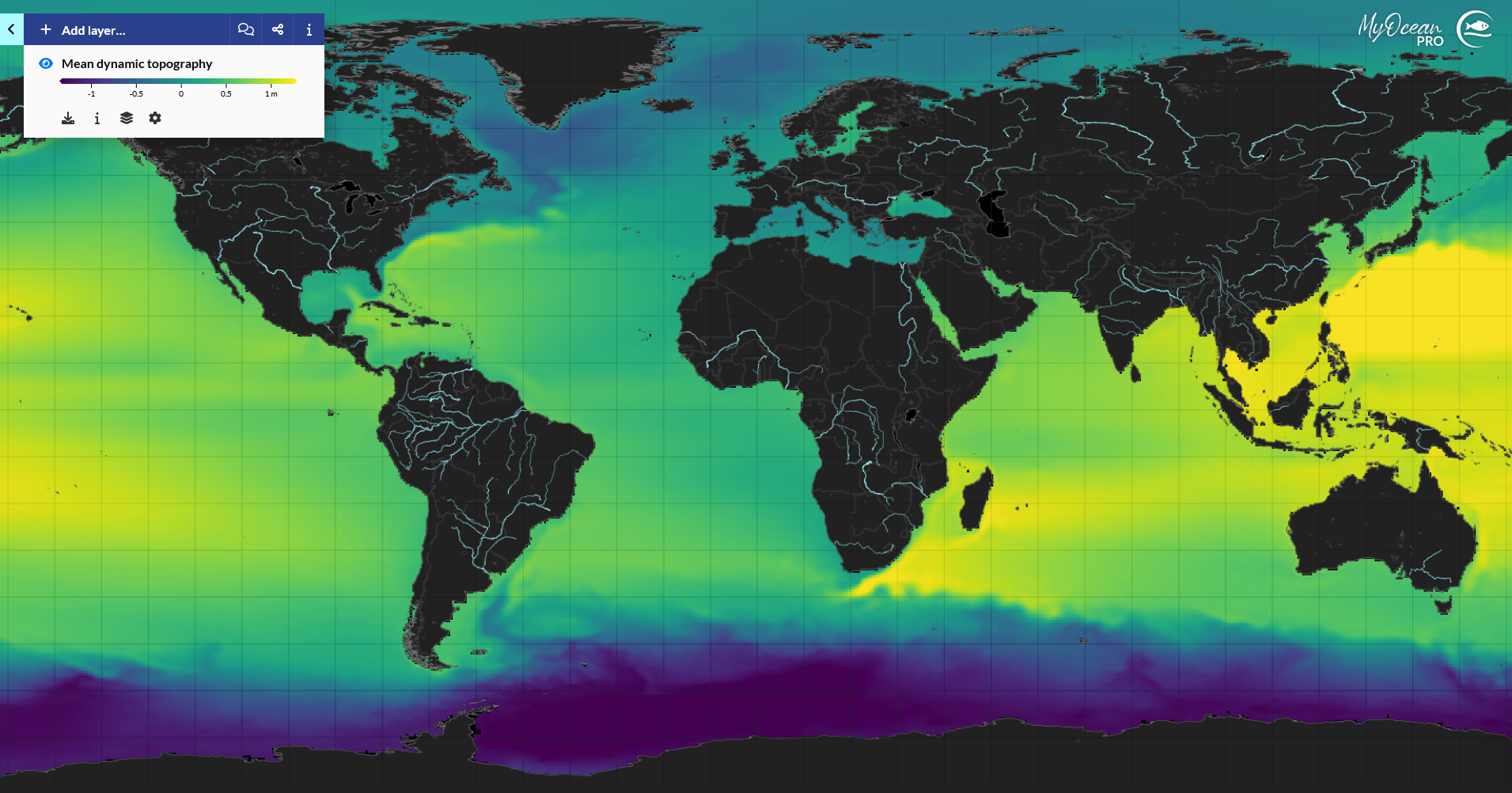
Wir sehen, dass wir tatsächlich ein paar wichtige Strömungen wiedererkennen. Den Golfstrom zum Beispiel oder den antarktischen Zirkumpolarstrom. Das zeigt, dass viele dieser Strömungen geostrophisch sind und man sie näherungsweise gut mit dieser einfachen Formel ausrechnen kann.

Zu Zeiten von Ekman gab es allerdings noch keine Satelliten. In der “dynamischen Theorie” muss man die Meeresspiegelhöhe also anders bestimmen. Dazu sehen wir uns nochmal ein Bild aus Vorlesung 4 an:

Die Meeresspiegelhöhe kann man ausrechnen, wenn man annimmt, dass am Boden kein Druckgradient existiert.

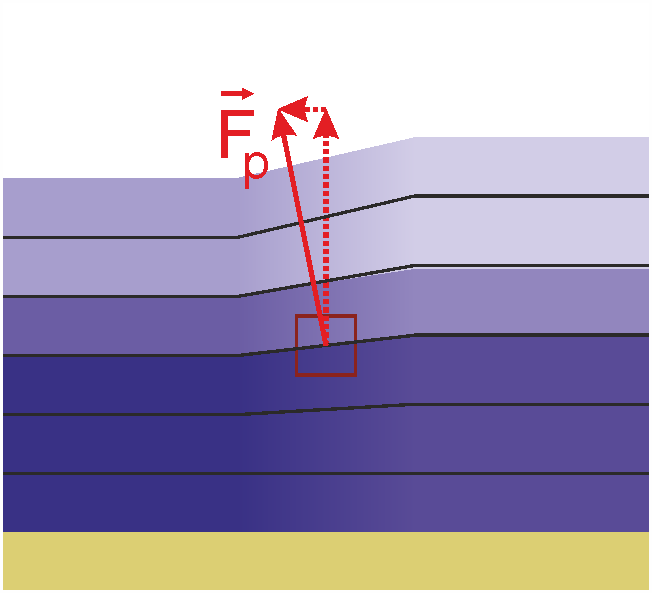
Wenn man annimmt, dass am Boden kein Druckgradient sein soll, dann kann man die Meeresspiegelhöhe aus der Dichte $\rho$ ausrechnen. Es muss einfach die gleiche Masse an Wasser auf jedem Quadratmeter liegen, trotz verschiedener Dichte. Genau das ist die “dynamische Theorie”: Wir messen die Dichte, ermitteln die Meeresspiegelhöhe, berechnen den Druckgradienten und kennen dann näherungsweise die Strömung.

Wie wir sehen, treten die stärksten Gradienten ja auch tatsächlich da auf, wo Wasser verschiedener Dichte aufeinandertrifft:

• Beim Golfstrom oder beim antarktischen Zirkumpolarstrom gibt es Sprünge in der Temperatur.

• Beim Norwegischen Küstenstrom gibt es Unterschiede im Salzgehalt.

Die mittlere Meeresspiegelhöhe über dem Geoid in Nordeuropa, 1993-2012, aus Satellitenmessungen.
[https://data.marine.copernicus.eu/product/SEALEVEL_GLO_PHY_MDT_008_063/description]

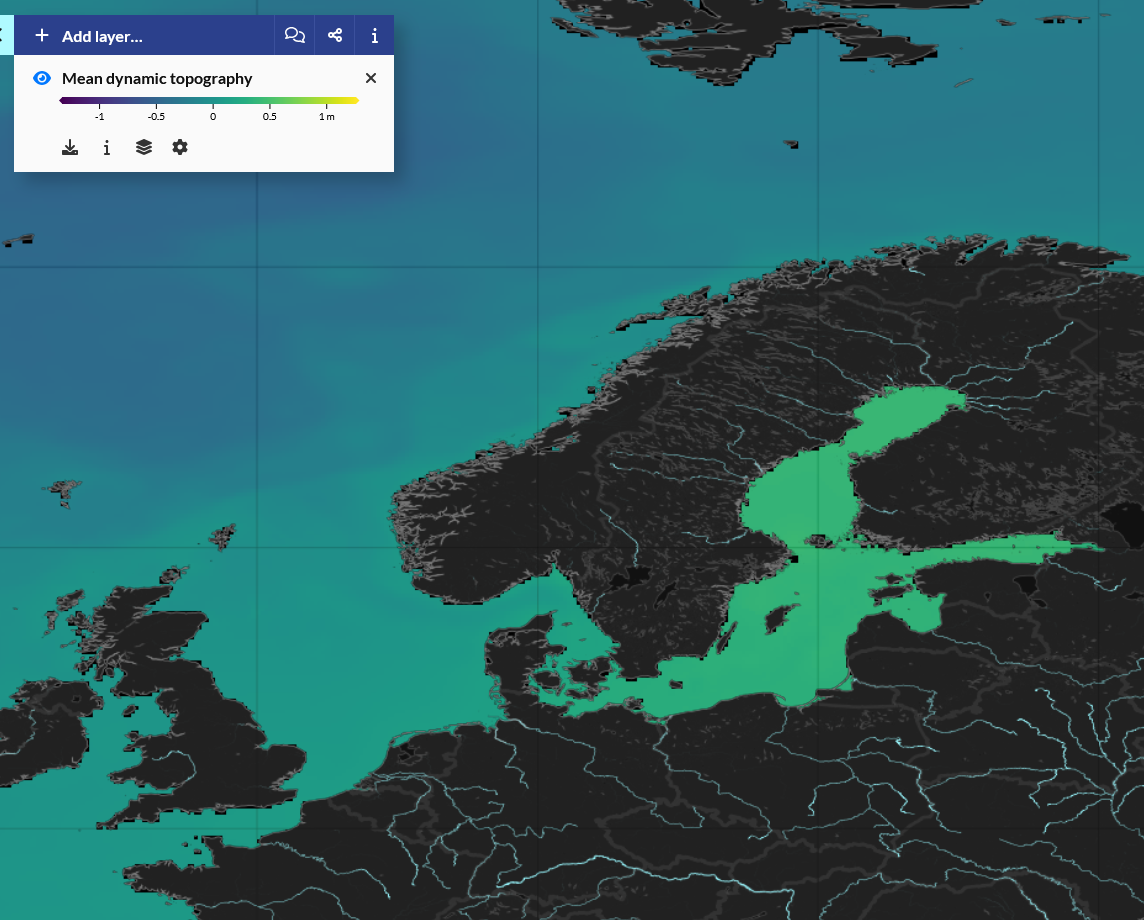
Damit haben wir einen wesentlichen Mechanismus verstanden, wie Meeresströmungen entstehen: Das Wasser will “bergab” fließen, wird aber von der Corioliskraft um 90° abgelenkt und fließt stattdessen parallel zum “Hang” entlang. Bei dieser Strömung wirkt die Corioliskraft nun hangaufwärts und die Druckgradientenkraft hangabwärts, so dass die Kräfte sich ausgleichen. Da also keine Beschleunigung erzeugt wird, kann das Wasser mit der gleichen Geschwindigkeit weiter strömen.

Im Weiteren Verauf der Vorlesung werden wir uns

• Beispiele für geostrophische Strömungen ansehen und

• windgetriebene Strömungen ansehen als anderen wichtigen Mechanismus.

<– Zurück zur Übersicht