
Euler und Lagrange messen die Temperatur im Fluss.

Als nächstes wollen wir betrachten, wie sich die Temperatur an einem Ort im Meer ändert.
Betrachten wir zunächst mal eine kleine Skizze:

Wer von beiden hat Recht? Natürlich jeder irgendwie, denn sie messen zwei verschiedene Sachen. Bei Herrn Euler strömt das kalte Wasser aus der Schneeschmelze heran, deswegen wird es da, wo er steht, immer kälter. Herr Lagrange bewegt sich mit dem Wasser mit, und weil die Sonne scheint, wird es immer wärmer.
Wir möchten uns das ganze mal physikalisch ansehen. Nehmen wir mal an, wir haben ein Thermometer in einem Mooring verbaut. Das misst kontinuierlich die Temperatur. Und die erhöht sich, weil die Sonne scheint. Aber das ist nicht der einzige Grund. Außerdem strömt das Wasser von links nach rechts (von West nach Ost), und auf der linken Seite ist es wärmer. (Im Gegensatz zu Herrn Eulers Flusswasser.)
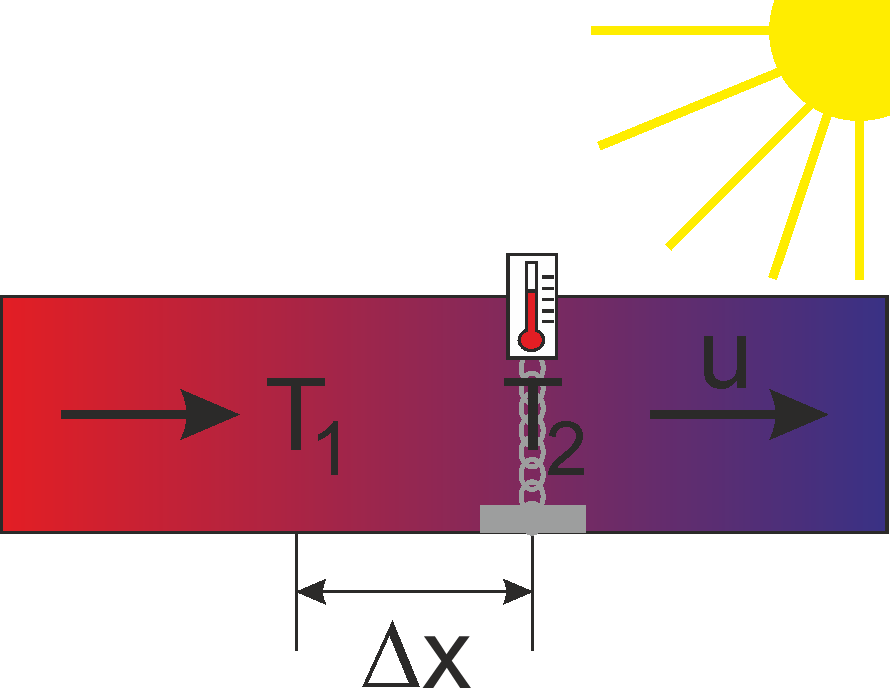
Wir haben zunächst mal also eine Erwärmung, die rein aufgrund der Strömung zustande kommt:
\[ \frac{\partial T}{\partial t} = - u \cdot \frac{\partial T}{\partial x} + \dots \]
Zu dieser Erwärmung kommt noch eine weitere hinzu, nämlich die durch die Sonne. Die Änderung in einem mitgeführten Volumen nennen wir \(\frac{\mathrm{D}}{\mathrm{D}t}\).
\[ \frac{\partial T}{\partial t} = - u \cdot \frac{\partial T}{\partial x} + \frac{\mathrm{D}T}{\mathrm{D}t} \]
Diese Gleichung beschreibt, wie sich lokal an einem festen Ort eine Größe ändert. Das bezeichnen wir als “Eulersche Perspektive”.
Die Größe \(\frac{\mathrm{D}T}{\mathrm{D}t}\) hingegen beschreibt, wie sich die Temperatur in einem von der Strömung mitgeführten Wasserpaket ändert. Die ist viel relevanter, denn Änderungen (wie Erwärmung, aber auch Beschleunigung durch Krafteinwirkung) wirken natürlich auf Wasserpakete und nicht auf Orte. Wir können nach ihr umstellen:
\[ \frac{\mathrm{D}T}{\mathrm{D}t} = \frac{\partial T}{\partial t} + u \cdot \frac{\partial T}{\partial x} \]
Allgemein könnte die Strömung natürlich aus mehreren Richtungen kommen.
\[ \frac{\mathrm{D}T}{\mathrm{D}t} = \frac{\partial T}{\partial t} + u \cdot \frac{\partial T}{\partial x} + v \cdot \frac{\partial T}{\partial y} + w \cdot \frac{\partial T}{\partial z} \] \[ \frac{\mathrm{D}T}{\mathrm{D}t} = \frac{\partial T}{\partial t} + \vec{u} \cdot \left( \vec{\nabla} T \right) \]
Im allgemeinen bezeichnen wir den Operator
\[ \frac{\mathrm{D}}{\mathrm{D}t} = \frac{\partial }{\partial t} + \vec{u} \cdot \vec{\nabla} \]
als Eulersche Ableitung oder materielle Ableitung. Ein mitgeführtes Wasserpaket und dessen Änderungen zu betrachten, ist die “Lagrangesche Perspektive”.
Die Eulersche Ableitung ist der Schlüssel dazu, die Gleichungen zu formulieren, die die Strömung im Meer erklären. Denn die Wasserpakete ändern nicht nur ihre Eigenschaften, wie Temperatur. Sie können auch ihre Bewegung ändern, also beschleunigt werden. Und das geschieht nach dem 2. Newtonschen Axiom, wenn eine Kraft auf das Wasserpaket einwirkt.
Betrachten wir dazu ein Wasserpaket mit einem Volumen \(\Delta V\). Es hat eine Dichte \(\rho\) und damit eine Masse
\[ \Delta m = \rho \cdot \Delta V \]
Nehmen wir mal an, auf dieses Wasserpaket wirkt eine Kraft \(\Delta F\). Die wird gemessen in Newton (N). Dann wird es beschleunigt mit
\[ a = \frac{\Delta F}{\Delta m} = \frac{1}{\rho} \cdot \frac{\Delta F}{\Delta V} \]
Für die Beschleunigung sind also zwei Größen entscheidend:
die Dichte \(\rho\)
die Kraftdichte \(\Delta F / \Delta V\) (gemessen in Newton pro Kubikmeter, N/m\(^3\)).
Hier können wir wieder mal den Grenzübergang machen und ein unendlich kleines Wasservolumen annehmen, dann heißt die Kraftdichte
\[ \frac{\mathrm{d}F}{\mathrm{d}V} \]
Und der Physiker bezeichnet die irreführend wieder mal als \(F\), oder noch besser als \(\vec{F}\), da sie ja eine Richtung hat. Auch wir werden das so machen und mit \(\vec{F}\) eine Kraftdichte bezeichnen. Wir erhalten dann:
\[ \vec{a} = \frac{1}{\rho} \cdot \vec{F} \]
Und was ist die Beschleunigung \(\vec{a}\)? Das ist die Bewegungsänderung eines Wasserpakets. Hier brauchen wir also die Eulersche Ableitung:
\[ \frac{\mathrm{D} \vec{u}}{\mathrm{D} t} = \frac{1}{\rho} \cdot \vec{F} \]
Ausgeschrieben lautet das:
\[ \frac{\partial \vec{u}}{\partial t} + \left( \vec{u} \cdot \vec{\nabla} \right) \vec{u} = \frac{1}{\rho} \cdot \vec{F} \]
Wir verschieben den advektiven Anteil auf die rechte Seite, indem wir ihn subtrahieren.
\[ \frac{\partial \vec{u}}{\partial t} = - \left( \vec{u} \cdot \vec{\nabla} \right) \vec{u} + \frac{1}{\rho} \cdot \vec{F} \]
Was sagt die Gleichung aus?
Die linke Seite gibt an, wie schnell sich die Strömung an einem bestimmten, festen Punkt im Meer ändert.
Die rechte Seite sagt, dass es zwei Anteile gibt.
Der erste Summand sagt, dass die Strömung sich dort ändert, wenn Wasser mit anderer Geschwindigkeit heranströmt. (Ja, auch die Strömung selbst kann heranströmen).
Der zweite Summand ist die Beschleunigung der Strömung durch Kräfte, die auf das Wasser einwirken.
Zwei Dinge kann man mit dieser Gleichung anfangen:
Man kann vorhersagen, wie die Strömung in der Zukunft wird. Denn wenn man die Strömung, die Dichte und die wirkenden Kräfte kennt, kann man die rechte Seite ausrechnen. Dann weiß man, wie die Strömung sich ändert, und kann ein kleines Stück in die Zukunft rechnen. Das ist das Prinzip wie Ozeanmodelle funktionieren. Die berechnen diese Änderung der Strömung immer und immer wieder für kleine Zeitschritte.
Man kann sich für stationäre Strömungen interessieren. Das heißt, solche, die immer an der gleichen Stelle sind. Dann ist die linke Seite null, weil sich ja vor Ort nichts ändert. Dann kann man, wenn man die Dichte gemessen hat und die Kräfte kennt, versuchen, die Strömung \(\vec{u}\) zu berechnen. Das ist der Hintergrund der “dynamischen Methode” von Ekman, die in der ersten Vorlesung erwähnt wurde.
Nun müssen wir erst mal wissen, welche Kräfte denn im Meer wirken und wichtig sind. Das wird die nächsten Vorlesungen umfassen, uns diese Kräfte anzusehen.
Hier in der Vorlesung werden wir uns vier verschiedene Kräfte ansehen. Diese wären:
\(\vec{F}_w\): Windschub
\(\vec{F}_g\): Gewichtskraft
\(\vec{F}_p\): Druckgradientenkraft
\(\vec{F}_r\): Reibungskraft
\(\vec{F}_c\): Corioliskraft (das ist gar keine echte Kraft, sondern nur eine Scheinkraft, die auf der rotierenden Erde auftritt)
Der Wind ist meist viel schneller als die Meeresströmung an der Oberfläche. Darum beschleunigt er das Meer näherungsweise in Windrichtung.
Eigentlich wirkt er nur an der Oberfläche. Aber eine Deckschicht ist gut durchmischt, von den Oberflächenwellen. Das können mal nur 10 m sein oder auch 60 m, je nachdem, wieviel Wind schon vorher war.
Dann kann man näherungsweise annehmen, dass die Kraft des Windes gleichmäßig auf diese Deckschicht wirkt. Und natürlich nur in horizontaler Richtung. Hier gilt:
\[ \vec{F}_w = \begin{pmatrix} X \\ Y \\ 0 \end{pmatrix} \]
Zur Erinnerung: Wir verwenden eigentlich wieder eine Kraftdichte (Einheit: Newton pro Kubikmeter).
Unterhalb der durchmischten Schicht ist der Windschub null.
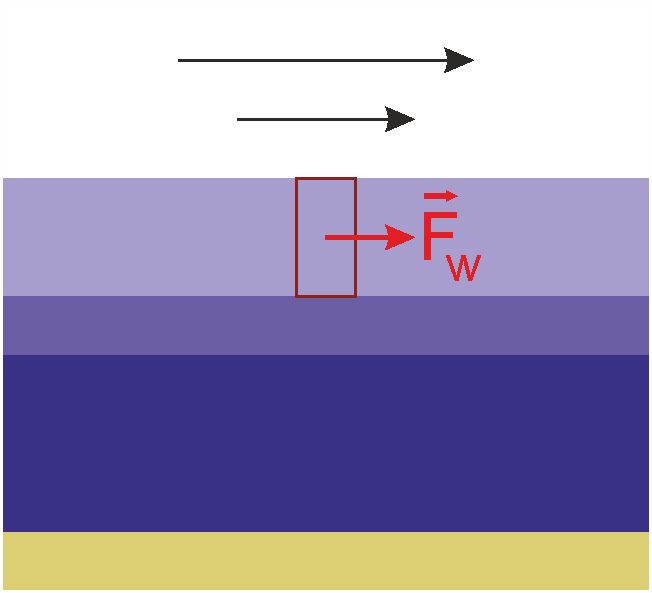
Der Windschub steigt quadratisch mit der Windgeschwindigkeit an. Bei doppeltem Wind gibt es also den vierfachen Windschub.
Die Gewichtskraft versucht, Masse in Richtung Erdmittelpunkt zu ziehen.
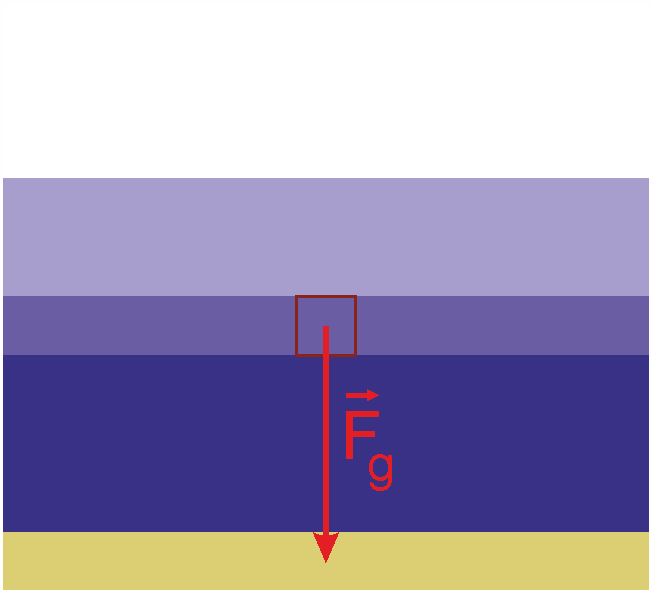
Nehmen wir ein Wasserpaket der Größe \(\Delta V\). Das hat eine Masse von
\[ \Delta m = \rho \cdot \Delta V \]
und eine Gewichtskraft von
\[ \Delta F_g = g \cdot \Delta m = g \cdot \rho \cdot \Delta V \]
Wir sind aber an der Kraftdichte interessiert, an \(\Delta F_g / \Delta V\). Hier kürzt sich das V heraus und wir erhalten als Kraftdichte:
\[ F_g = g \cdot \rho \]
Die Gewichtskraft wirkt nur vertikal und nach unten, also können wir schreiben:
\[ \vec{F}_g = \begin{pmatrix} 0 \\ 0 \\ - g \cdot \rho \end{pmatrix} \]
In der Praxis beschleunigt sie aber längst nicht so stark, weil, salopp gesprochen, das Wasser auf anderem Wasser aufliegt. Wir werden später sehen, dass sie sich mit einer anderen Kraft, der Druckgradientenkraft, näherungsweise ausgleicht.
Auch Sonne und Mond haben eine Anziehungskraft auf das Wasser. Das führt zu Gezeiten.
Ursache ist, dass die Anziehungskraft auf das Wasser auf verschiedenen Seiten der Erde verschieden stark ist.
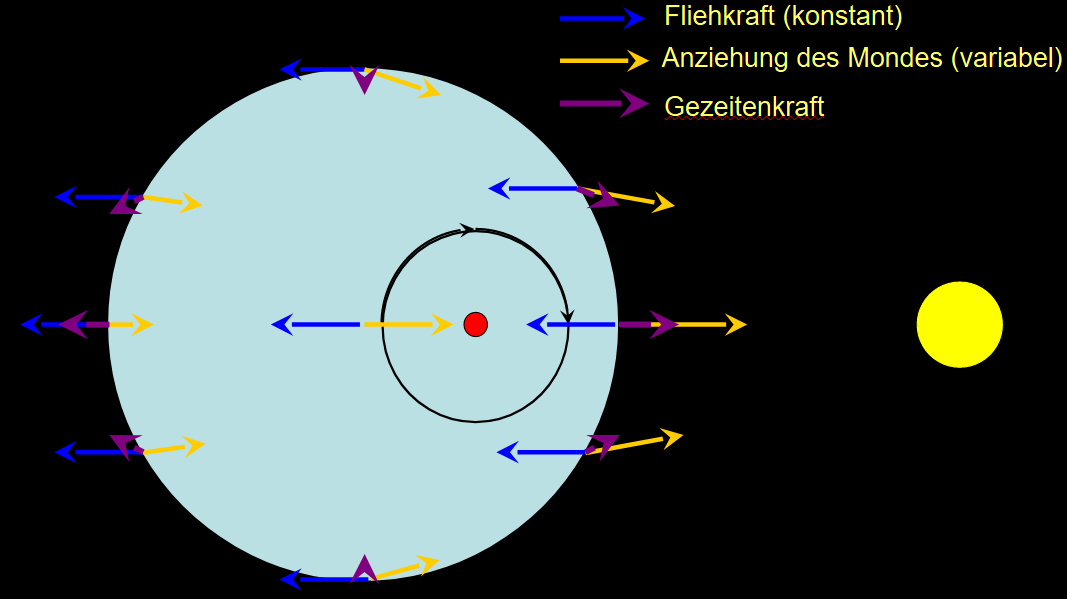
Die Anziehungskraft des Mondes auf das Meerwasser ist auf der mondzugewandten Seite stärker, auf der mondabgewandten Seite schwächer. Das führt in sehr vereinfachter Theorie zu zwei Wasserbergen, die synchron mit dem Mond um die Erde herumlaufen.
Dasselbe würde für die Sonne gelten, aber da ist der Effekt schwächer, weil die prozentuale Abweichung in der Entfernung zur Sonne recht klein ist.
In der Realität sind die Kontinente im Weg. So kommt es zu einem komplizierten Wellenmuster, das sich mit der anregenden Frequenz ausbreitet.
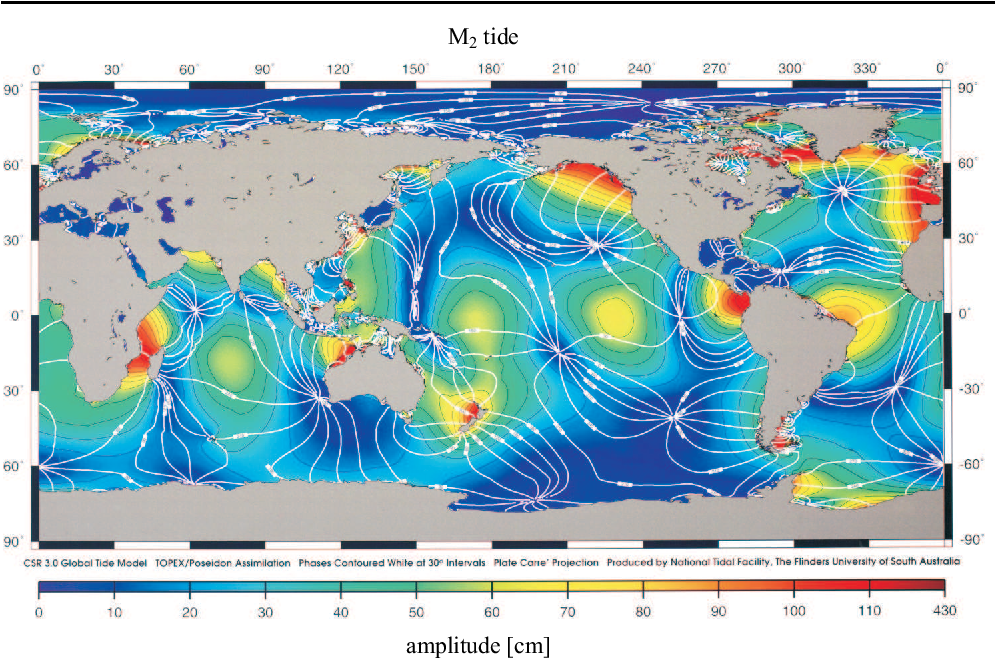
Die Höhe der Gezeiten ist also sehr unterschiedlich an verschieden Küstenabschnitten. Starke Gezeiten haben auch gravierende Auswirkungen auf das Ökosystem, weil sich zwei Dinge wesentlich ändern:
Kurze Residenzzeit: Wasser bleibt nicht lange an einem Ort, sondern wird weggespült
Hohe Bodenschubspannung: Die Strömung über den Grund ist regelmäßig stark, daher kann sich wenig feines Material ablagern.
Die Druckgradientenkraft beschleunigt das Wasser immer vom höheren zum niedrigeren Druck.
Wie wir den Druck ausrechnen können, wissen wir ja schon: Mit der hydrostatischen Näherung. Daher wissen wir, wie der Druck sich vertikal verändert. Verändert er sich nur vertikal, dann ist die Druckgradientenkraft nach oben gerichtet und wirkt der Gewichtskraft entgegen.
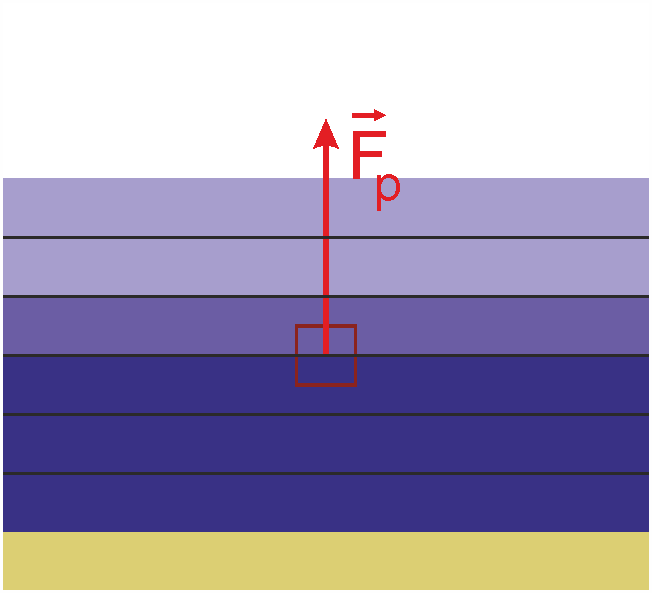
Aber wenn die Dichte sich horizontal ändert, ändert sich natürlich auch der Druck in der gleichen Tiefe. Dann treten horizontale Druckgradienten auf. In diesem Fall hat die Druckgradientenkraft auch eine horizontale Komponente. (Sie steht senkrecht auf den Isobaren, den Flächen gleichen Drucks.)
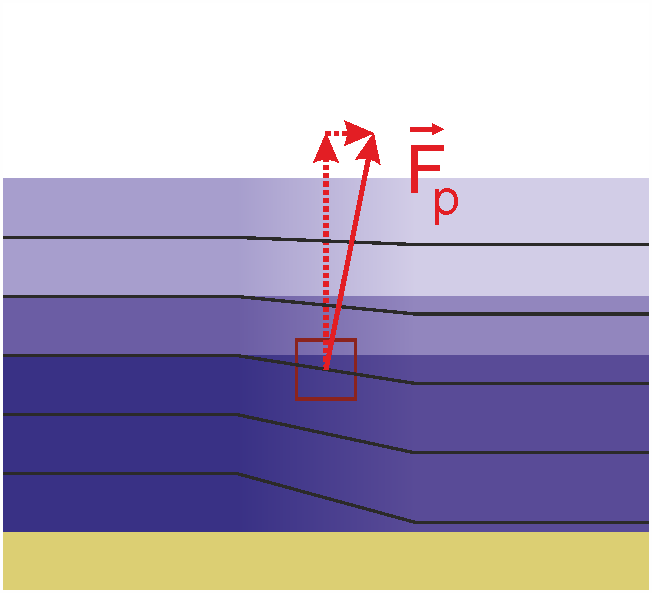
Eine weitere Möglichkeit, wie horizontale Druckgradienten entstehen, ist eine Auslenkung des Meeresspiegels. Also ein von Normal-Null (NN) verschiedener Wasserstand. Die Last des aufliegenden Wassers wirkt als Druck in der gesamten Wassersäule, und dieser zusätzliche Druck ist annähernd proportional zum Wasserstand.
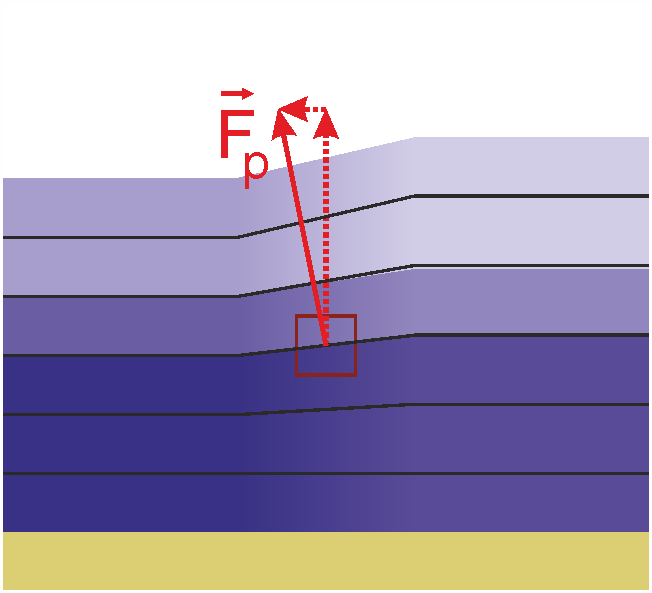
Dass die Kraft vom höheren zum niedrigeren Druck wirkt, kann man wie folgt schreiben:
\[ \vec{F}_p = \begin{pmatrix} -\frac{\partial p}{\partial x} \\ -\frac{\partial p}{\partial y} \\ -\frac{\partial p}{\partial z} \end{pmatrix} = - \vec{\nabla} \cdot p \]
In der \(z\)-Komponente steht die vertikale Änderung des Drucks. Die können wir ja aber schon näherungsweise ausrechnen - mit der hydrostatischen Näherung:
\[ \frac{\partial p}{\partial z} \approx - g \cdot \rho \]
Es ergibt sich also für die Druckgradientenkraft:
\[ \vec{F}_p = \begin{pmatrix} -\frac{\partial p}{\partial x} \\ -\frac{\partial p}{\partial y} \\ \approx g \cdot \rho \end{pmatrix} \]
Näherungsweise gleichen sich also Gewichtskraft und Druckgradientenkraft vertikal genau aus.
Wenn ein Wasserpartikel mit anderer Geschwindigkeit strömt als seine Umgebung, dann tritt eine Reibungskraft auf, die es dazu bringt, seine Geschwindigkeit der Umgebung anzugleichen.
Betrachten wir im Beispiel einen Ozean, der in der Mitte eine schnelle Strömung hat, darüber und darunter aber nicht.
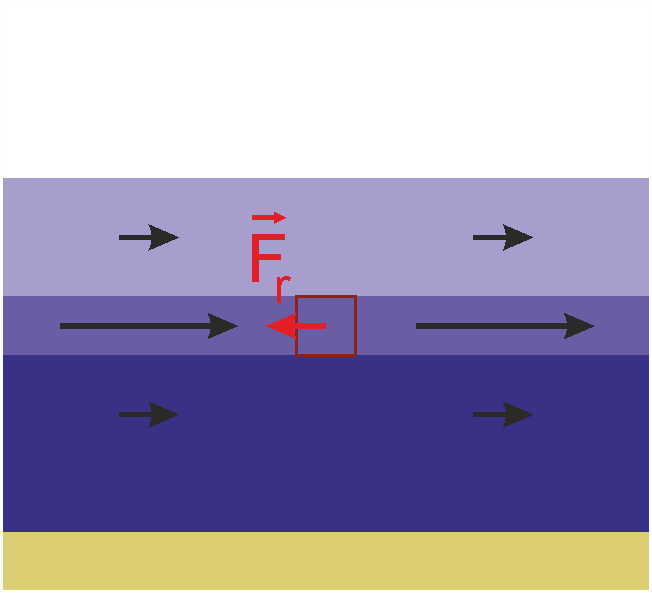
Hier würde die starke Strömung in der mittleren Schicht nach und nach von der Reibung gebremst werden. Die darüber und darunter liegenden Schichten würden hingegen beschleunigt.
Mathematisch brauchen wir die zweite Ableitung, um den Unterschied zu der Umgebung darüber und darunter auszudrücken. In unserem Beispiel gilt:
\[ F_{r,x} = \rho \nu_z \frac{\partial^2 u}{\partial z^2} \]
Hierbei beschreibt der Reibungskoeffizient \(\nu_z\), wie stark die innere Reibung in \(z\)-Richtung ist.
Praktisch kann Reibung aber in alle drei Richtungen auftreten:
\[ F_{r,x} = \rho \nu_x \frac{\partial^2 u}{\partial x^2} + \rho \nu_y \frac{\partial^2 u}{\partial y^2} + \rho \nu_z \frac{\partial^2 u}{\partial z^2} \]
Das Wasser wird abgebremst, wenn es schneller ist als
das Wasser östlich und westlich (mit Stärke \(\nu_x\)),
das Wasser nördlich und südlich (mit Stärke \(\nu_y\)),
das Wasser darüber und darunter (mit Stärke \(\nu_z\)).
In der Praxis ist der horizontale Reibungskoeffizient dabei etwa 1000 mal stärker, wir haben
| Formelzeichen | Größe | Größenordnung |
|---|---|---|
| \(\nu_x,\:\nu_y\) | Horizontale effektive Viskosität | 1-100 m²/s |
| \(\nu_z\) | Vertikale effektive Viskosität | ~0.001 m²/s |
| \(\nu\) | molekulare Viskosität | 0.000001 m²/s |
Die molekulare Viskosität kann man im Labor messen. Die beschreibt, dass Wasser eigentlich ziemlich wenig zäh ist (auch im Vergleich mit anderen Flüssigkeiten), also nur eine sehr kleine Viskosität hat.
Warum ist nun das Meer so viel zäher? Das liegt an der Turbulenz.
Turbulenz heißt, es bilden sich zufällige Verwirbelungen. Die tauschen Wasser zwischen angrenzenden Schichten aus, oder auch horizontal. Und damit mischen sie auch die Eigenschaften des Wassers. Zum Beispiel die Geschwindigkeit (oder, wie der Physiker präziser sagt, den Impuls).
Diese Wirbel zerfallen nach und nach in immer kleinere Wirbel. Wenn sie auf der Millimeter-Skala angekommen sind, werden sie von der molekularen Viskosität gebremst und verschwinden, ihre Energie wird dann Wärme.
Weil die Wirbel sich einfacher horizontal drehen können als vertikal, ist die horizontale turbulente Viskosität so hoch. Vertikal müssten sie schwereres Wasser anheben, d.h. Schichtung bremst die Turbulenz aus.
Die vertikale Vermischung ist der zweite wichtige Effekt der Turbulenz. Auch Inhaltsstoffe wie Salz oder Nährstoffe und Wärme werden durch die Turbulenz vermischt, horizontal und vertikal.
Aber weil die Turbulenz durch Schichtung behindert wird, ist der vertikale Austausch zwischen Schichten verschiedener Dichte stark gehemmt. Thermokline oder Halokline bilden so oft auch Trennschichten zwischen biologisch sehr verschiedenen Wassermassen (Sauerstoffgehalt, Nährstoffgehalt).