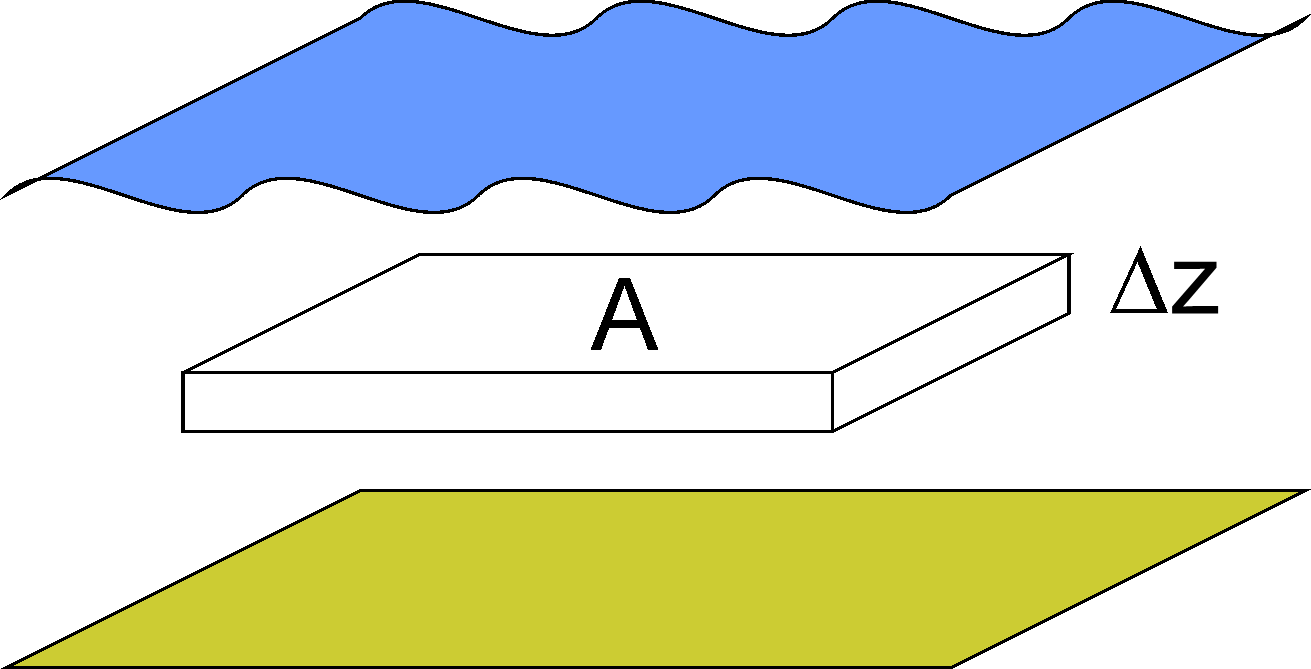
Ein kleines Wasservolumen \(A \cdot \Delta z\)

Druck beschreibt in der Physik, wenn eine Kraft nicht auf einen Punkt, sondern gleichmäßig auf eine Fläche einwirkt. Dann ist der Druck das Verhältnis zwischen Kraft und Fläche:
\[ p = \frac{F}{A} \]
Den Druck im Wasser kann man meistens gut mit der hydrostatischen Näherung ausrechnen. Dabei betrachten wir die Kraft, die auf eine horizontale Fläche im Meer einwirkt, in der Tiefe \(z\). Das ist von oben die Gewichtskraft
\[ F = m \cdot g \]
Dabei ist \(g\) die Fallbeschleunigung, \(g = 9.81\)ms\(^{-2}\). Die Masse ist die Masse der Atmosphäre und die Masse des darüberliegenden Wassers. Beide machen jeweils einen Druck der sich addiert:
\[ p = p_A + p_W = p_A + \frac {m \cdot g}{A} \]
Wenn das Wasser eine konstante Dichte \(\rho\) hat, ist das einfach. Dann ist \(m = \rho \cdot A \cdot z\) und wir erhalten
\[ p_W = \rho \cdot z \cdot g \]
Wir sehen, dass wir deshalb Druck und Tiefe näherungsweise sehr einfach ineinander umrechnen können. Da die Dichte von Meerwasser ( \(\approx 1025\,\frac{\mathrm{kg}}{\mathrm{m}^3}\) ) und die Fallbeschleunigung (\(9.81\,\frac{\mathrm{m}}{\mathrm{s}^2}\) ) als Produkt ungefähr 10000 ergeben, gilt, dass 1 m Wassertiefe ungefähr 10000 Pa an Druck ausmacht, oder 1 dbar.
Leider ändert sich die Dichte oft mit der Tiefe, und wir haben oben leichteres und unten schwereres Wasser. Dann schauen wir uns mal an, wie sich der Druck über eine dünne Schicht ändert:

\[ p_{unten} = p_{oben} + \rho(z) \cdot \Delta z \cdot g \]
oder anders geschrieben:
\[ \frac{\Delta p}{\Delta z} = \rho(z) \cdot g \]
Wir können nun unser \(\Delta z\) unendlich klein machen (Grenzübergang):
\[ \frac{\mathrm{d} p}{\mathrm{d} z} = \rho(z) \cdot g \]
Was haben wir denn hier? \(\rho(z)\) und \(p(z)\) sind beides Funktionen von der Tiefe \(z\). Auf der linken Seite steht eine Ableitung ( \(\frac{\mathrm{d} p}{\mathrm{d} z}\) ). Die Ableitung des Drucks ist also \(g\) mal die Dichte.
Das haben wir schon mal gesehen. Das heißt, dass der Druck die Stammfunktion der Dichte ist, bis auf den Faktor \(g\).
Wir nutzen jetzt mal den Hauptsatz der Differential- und Integralrechnung:
\[ A = \int\limits_{x=x_1}^{x_2} f(x) \cdot \mathrm{d} x = F(x_2) - F(x_1) \]
\(F\) ist also \(p\) und \(f\) ist \(\rho \cdot g\). Das setzen wir mal ein:
\[ A = \int\limits_{z=z_1}^{z_2} \rho(z) \cdot g \cdot \mathrm{d} z = p(z_2) - p(z_1) \]
Okay, wir wissen also, wie wir den Druckunterschied zwischen zwei Punkten ausrechnen. Wir müssen nur integrieren. Praktischerweise sagen wir mal, dass \(z_1\) and der Meeresoberfläche \(z=0\) sein soll, da ist \(p=p_A\).
\[ g \cdot \int\limits_{z=0}^{z_2} \rho(z) \cdot \mathrm{d} z = p(z_2) - p_A = p_W \]
Beispiel: \(\rho\) nimmt mit der Tiefe zu. Wir haben 10 m Wassertiefe.
\[ \rho = 1000\,\frac{\mathrm{kg}}{\mathrm{m}^3}+ 2\,\frac{\mathrm{kg}}{\mathrm{m}^4}\cdot z \]
Wie hoch ist der Druck am Meeresboden? Wir lassen mal die Einheiten der Einfachheit halber weg.
\[ p_W = g \cdot \int\limits_{z=0}^{10} \rho(z) \cdot \mathrm{d} z \]
\[ p_W = g \cdot \int\limits_{z=0}^{10} 1000 \cdot \mathrm{d} z + g \cdot \int\limits_{z=0}^{10} 2\cdot z \cdot \mathrm{d} z \]
\[ p_W = g \cdot \left[ 1000 \cdot z \right]_0^{10} + g \cdot \left[ z^2 \right]_0^{10} \]
\[ p_W = g \cdot (1000 \cdot 10-1000 \cdot 0) + g \cdot (10^2 - 0^2) \]
\[ p_W = 9.81 \cdot (10000 + 100) \]
\[ p_W = 99081~\mathrm{Pa} \]
Wasser ist nur näherungsweise inkompressibel. Sein Volumen nimmt bei höherem Druck ab, seine Dichte nimmt zu.
Mit der Volumenänderung einher geht eine Erwärmung beim Absinken und eine Abkühlung beim Aufsteigen. (So ähnlich wie bei Luft, es wird ja Arbeit verrichtet.)
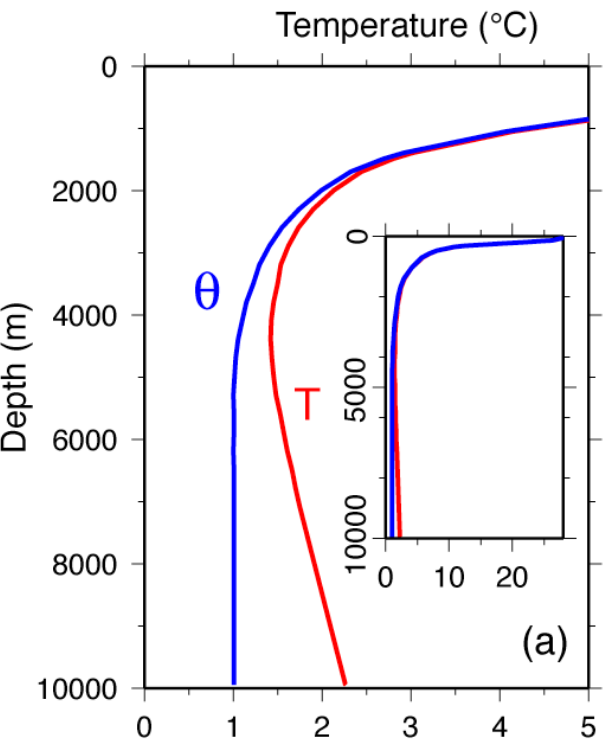
Potentielle Dichte und potentielle Temperatur beschreiben die Dichte (bzw. Temperatur), den eine Wassermasse hat, wenn man sie an die Meeresoberfläche hochholt, und zwar so schnell, dass es keine Wärme mit dem umgebenden Wasser austauschen kann. Im Gegensatz dazu ist die in-situ-Temperatur die, die man mit einem Thermometer in der Tiefe messen kann.
Ein Vektor ist in der Physik eine Größe, die einen Betrag und einen Richtung hat.
(In der Mathematik wird er anders definiert, da definiert man die Eigenschaften des Vektorraums als einer Menge von Vektoren).
Üblicherweise hat man in der Physik also dreidimensionale Vektoren, weil es drei Raumrichtungen gibt.
Man schreibt die Vektoren gern in der Indexschreibweise, z.B.:
\[ \vec{v} = \begin{pmatrix} a \\ b \\ c \end{pmatrix} = \begin{pmatrix} 3 \\ 2 \\ 5 \end{pmatrix} \]
Das kann man nur machen, wenn man vorher ein Koordinatensystem festgelegt hat, mit \(x\)- \(y\)- und \(z\)-Achse.
In dem Koordinatensystem gibt es dann spezielle Vektoren, die Einheitsvektoren:
\[ \vec{e}_x, \: \vec{e}_y, \: \vec{e}_z \]
Die haben eine Länge von 1 und zeigen entlang der entsprechenden Achse.
Unser Beispielvektor \[ \vec{v} = \begin{pmatrix} 3 \\ 2 \\ 5 \end{pmatrix} \] ist dann ein zusammengesetzter Vektor
\[ \vec{v} = 3 \cdot \vec{e}_x + 2 \cdot \vec{e}_y + 5 \cdot \vec{e}_z \].
Was man hier schon sieht, ist, dass man Vektoren addieren kann, und man kann sie auch mit Zahlen multiplizieren. Beim Addieren kann man ein Parallelogramm malen, um den Summenvektor zu erhalten.
Vektoren in der Physik können auch Einheiten haben, z.B. m (Meter) wenn sie einen Ort beschreiben oder m/s wenn sie eine Geschwindigkeit beschreiben.
Die Länge eines Vektors ergibt sich aus dem Satz des Pythagoras:
\[ | \vec{v} | = v = \sqrt{a^2 + b^2 + c^2} \]

Wenn man rausfinden will, ob Vektoren senkrecht aufeinander stehen (also einen Winkel von 90° haben), kann man das Skalarprodukt nutzen. Das geht ganz einfach zu berechnen:
\[ \begin{pmatrix} a \\ b \\ c \end{pmatrix} \cdot \begin{pmatrix} d \\ e \\ f \end{pmatrix} = a \cdot d + b \cdot e + c \cdot f \]
Wie man sieht kommt da eine Zahl raus. Was bedeutet die Zahl?
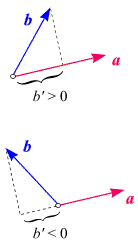
Wir spalten den zweiten Vektor auf, in einen Anteil, der zum ersten Vektor parallel ist, und einen zweiten Anteil der zum ersten Vektor senkrecht ist. Und die Längen der beiden parallelen Vektoren multiplizieren wir. Und wenn es nun gar keinen parallelen Anteil gibt, weil der Vektor schon vorher senkrecht war, dann ist das Skalarprodukt null.
In der Ozeanographie verwenden wir üblicherweise folgendes Koordinatensystem:
| Achse | Vektor | zeigt nach |
|---|---|---|
| x-Achse | \(\vec{e}_x\) | Osten |
| y-Achse | \(\vec{e}_y\) | Norden |
| z-Achse | \(\vec{e}_z\) | oben |
Der Ursprung des Koordinatensystems liegt immer auf der Meeresoberfläche. Das heißt natürlich, die \(z\)-Koordinate ist im Meer immer negativ. In einer Tiefe von 20 m ist sie \(-20\).
Beispiel: Wir haben einen Wind etwa aus Südwest
\[ \vec{u}_A = \begin{pmatrix} 3\,\frac{\mathrm{m}}{\mathrm{s}} \\ 4\,\frac{\mathrm{m}}{\mathrm{s}} \\ 0\,\frac{\mathrm{m}}{\mathrm{s}} \end{pmatrix} \]
Die Strömung an der Oberfläche beträgt
\[ \vec{u} = \begin{pmatrix} 0.2\,\frac{\mathrm{m}}{\mathrm{s}} \\ -0.15\,\frac{\mathrm{m}}{\mathrm{s}} \\ 0\,\frac{\mathrm{m}}{\mathrm{s}} \end{pmatrix} \]
Wie schnell sind Wind und Strömung?
Wir rechnen
\[ | \vec{u}_A | = \sqrt{3^2 + 4^2 + 0^2}\,\frac{\mathrm{m}}{\mathrm{s}} = \sqrt{25}\,\frac{\mathrm{m}}{\mathrm{s}} = 5\,\frac{\mathrm{m}}{\mathrm{s}} \] \[ | \vec{u} | = \sqrt{0.2^2 + (-0.15)^2 + 0^2}\,\frac{\mathrm{m}}{\mathrm{s}} = \sqrt{0.0625}\,\frac{\mathrm{m}}{\mathrm{s}} = 0.25\,\frac{\mathrm{m}}{\mathrm{s}} \]
Der Wind weht mit 5 m/s und die Strömung strömt mit 25 cm/s.
In welchem Winkel stehen Wind und Strömung?
Wir lassen die Einheit weg und rechnen
\[ \vec{u}_A \cdot \vec{u} = 3 \cdot 0.2 - 4 \cdot 0.15 + 0 \cdot 0 = 0.6 - 0.6 + 0 = 0 \]
Wind und Strömung bilden einen Winkel von 90°.
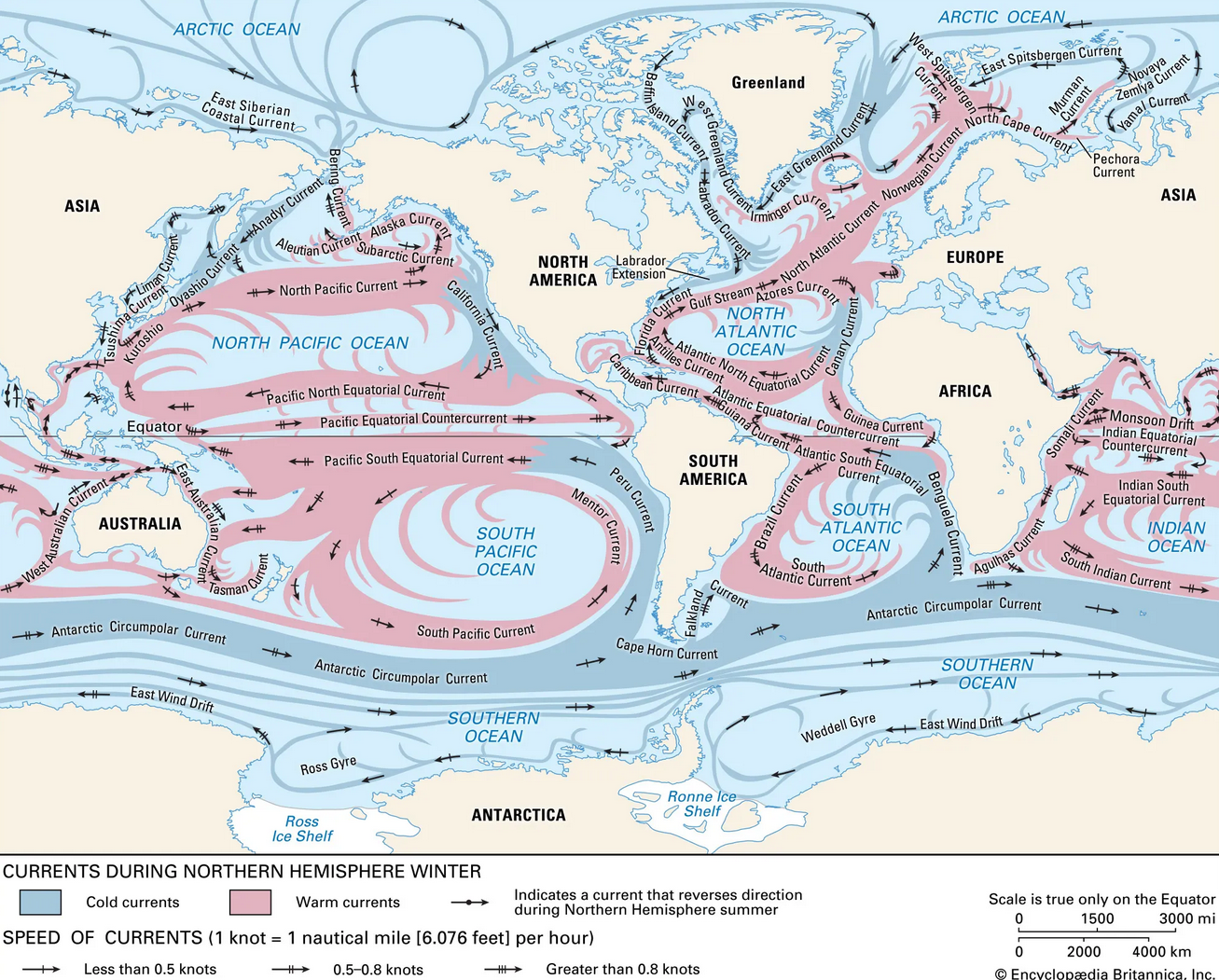
Die Geschwindigkeit von Meeresströmungen variiert stark. Oberflächenströmungen, die durch Wind angetrieben werden, erreichen typischerweise Geschwindigkeiten von 0.5 bis 3 km/h (unter 1 m/s). Der Golfstrom, einer der bekanntesten Meeresströmungen, kann an der Oberfläche Geschwindigkeiten von bis zu 1 m/s erreichen. In größeren Tiefen nimmt die Geschwindigkeit jedoch ab; bei etwa 2000 Metern Tiefe fließt das Wasser nur noch etwa zehnmal langsamer.
Die schnellsten Strömungen werden in bestimmten Regionen beobachtet, wie zum Beispiel im Antarktischen Zirkumpolarstrom, wo Geschwindigkeiten von über 2 m/s (ca. 7,2 km/h) erreicht werden können. Diese Strömung ist die größte und stärkste der Welt und umkreist die Antarktis.
Noch wesentlich stärkere Strömungen treten lokal durch Gezeitenströmungen auf. Der Saltstraumen gilt als der größte Gezeitenstrom der Welt und erreicht Geschwindigkeiten von bis zu 40 km/h. Er befindet sich zwischen den Fjorden Saltenfjorden und Skjerstadfjorden im Norden Norwegens. Die Strömungen entstehen durch die enge Passage, die das Wasser zwingt, sich schnell zu bewegen. Diese Strömung ist auch für Fischer von Bedeutung, da sie nährstoffreiches Wasser an die Oberfläche bringt. Ein Video darüber findet sich hier.
Die horizontale Geschwindigkeit von Meeresströmungen ist in der Regel höher als die vertikale Geschwindigkeit. Während Oberflächenströmungen durch den Wind stark beeinflusst werden und relativ schnell fließen, sind vertikale Strömungen oft langsamer. Vertikale Bewegungen, wie das Absinken von kaltem Wasser oder das Aufsteigen von warmem Wasser, geschehen häufig in einem Tempo von wenigen Zentimetern pro Sekunde.
Man unterscheidet barotrope Strömungen (die gesamte Wassersäule strömt in eine Richtung) und barokline Strömungen (unterschiedliche oder sogar gegenläufige Strömungsgeschwindigkeit in verschiedenen Tiefen).
Größen im Meer können in der physikalischen Ozeanographie als Feld aufgefasst werden. Weil sie räumlich und zeitlich veränderlich sind, hat das Feld drei Raumdimensionen und eine Zeitdimension.
Wichtige Felder wären:
| Größe | Bezeichnung | Einheit |
|---|---|---|
| Temperatur | \(T(x,y,z,t)\) | °C oder K |
| Salzgehalt | \(S(x,y,z,t)\) | g/kg |
| Dichte | \(\rho (x,y,z,t)\) | kg/m³ |
| Druck | \(p(x,y,z,t)\) | Pa oder dbar |
All diese können sich ändern, räumlich und mit der Zeit. Mathematisch beschreiben wir die Änderungen ja mit einer Ableitung. Hier können wir also mehrere Ableitungen bilden.
Zum Beispiel können wir messen, wie stark die Temperatur abnimmt, wenn man sich im Koordinatensystem nach Norden bewegt. Wir könnten schreiben
\[ \frac{\mathrm{d}T}{\mathrm{d}y} \]
aber um auszudrücken, dass sich nur \(y\) ändert und die anderen Koordinaten nicht, schreiben wir
\[ \frac{\partial T}{\partial y} \]
und nennen das partielle Ableitung. Genausogut könnten wir untersuchen, wie stark sich die Temperatur an immer demselben Ort mit der Zeit erwärmt:
\[ \frac{\partial T}{\partial t} \]
Wir machen ein Beispiel, wie eine partielle Ableitung funktioniert. Sei die Temperatur \(T\) gegeben durch
\[ T = 2x + 3xy \]
dann gilt:
\[ \frac{\partial T}{\partial x} = 2 + 3y \] \[ \frac{\partial T}{\partial y} = 3x \] \[ \frac{\partial T}{\partial z} = 0 \]
Bemerkung zur letzten Gleichung: Da die Berechnung von \(T\) nicht von \(z\) abhängt, kommt für unterschiedliche \(z\) immer dasselbe \(T\) heraus. In \(z\)-Richtung ist die Temperatur also konstant und ändert sich nicht. Daher ist die Ableitung \(\frac{\partial T}{\partial z}\) null.
Die Strömungsgeschwindigkeit ist ein besonderes Feld, weil sie eigentlich aus 3 Feldern besteht. Wir bezeichnen wie folgt:
| Bezeichnung | Bedeutung |
|---|---|
| \(u\) | Strömungsanteil nach Osten |
| \(v\) | Strömungsanteil nach Westen |
| \(w\) | Strömungsanteil nach oben |
| \(\vec{u} = \begin{pmatrix} u\\v\\w \end{pmatrix}\) | Strömungsvektor |
| \(|\vec{u}|\) | Strömungsgeschwindigkeit |
Der ganze Strömungsvektor kann wiederum in alle 4 Richtungen \(x\), \(y\), \(z\), \(t\) veränderlich sein, er bildet also ein Vektorfeld.
Die drei Komponenten des Strömungsvektors sind nicht unabhängig voneinander. Der Grund ist, dass strömendes Wasser in guter Näherung sein Volumen erhält.
Wir schauen uns einen quaderförmigen Bereich im Wasser an.
\[ \Delta V = \Delta x \cdot \Delta y \cdot \Delta z \]
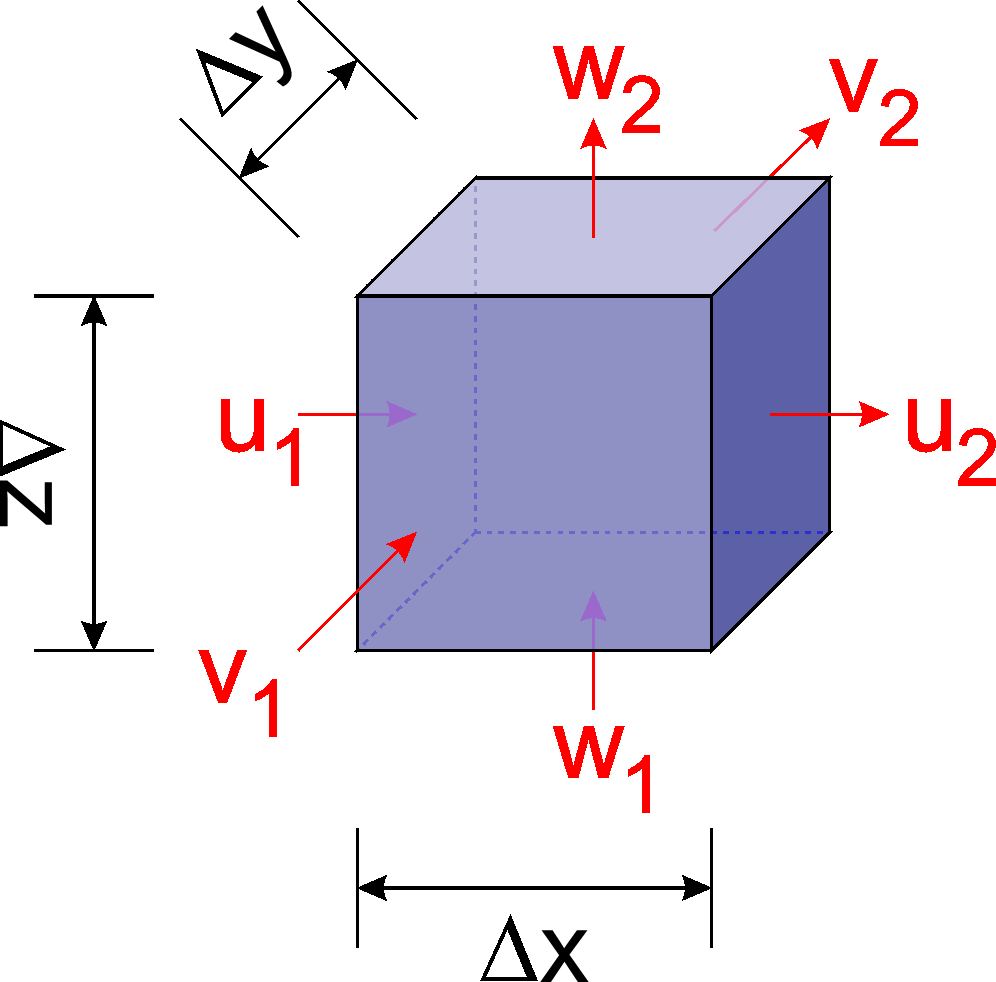
Wieviel Volumen strömt an der linken Seite herein? Wir haben ein mitteres \(u_1\), und auf der linken Seite herein strömt
\[ \Delta V_{links} = u_1 \cdot \Delta y \cdot \Delta z \cdot \Delta t \]
Rechts heraus strömt allerdings
\[ \Delta V_{rechts} = u_2 \cdot \Delta y \cdot \Delta z \cdot \Delta t \]
Also ergibt sich eine Differenz von
\[ \Delta V_x = (u_2 - u_1) \cdot \Delta y \cdot \Delta z \cdot \Delta t \]
die mehr herausströmt als herein. In den anderen Richtungen ist es ähnlich:
\[ \Delta V_y = (v_2 - v_1) \cdot \Delta x \cdot \Delta z \cdot \Delta t \] \[ \Delta V_z = (w_2 - w_1) \cdot \Delta x \cdot \Delta y \cdot \Delta t \]
Die Deltas können natürlich auch negativ sein, wenn in eine Richtung weniger aus- als einströmt. Volumenerhaltung bedeutet, dass in der Summe genau so viel einströmen wie ausströmen muss.
\[ \Delta V_x + \Delta V_y + \Delta V_z = 0 \]
Wir schreiben das aus und nennen die Differenzen in \(\Delta u\), \(\Delta v\), \(\Delta w\).
\[ \Delta u \cdot \Delta y \cdot \Delta z \cdot \Delta t + \Delta v \cdot \Delta x \cdot \Delta z \cdot \Delta t + \Delta w \cdot \Delta x \cdot \Delta y \cdot \Delta t = 0 \]
Wir dividieren durch das Volumen der Box und den Zeitschritt
\[ \frac{\Delta u}{\Delta x} + \frac{\Delta v}{\Delta y} + \frac{\Delta w}{\Delta z} = 0 \]
Wir können nun annehmen, dass die Box immer und immer kleiner wird. Im Grenzübergang ergibt sich
\[ \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z} = 0 \]
Wir sehen, die partiellen Ableitungen der Geschwindigkeitskomponenten haben hier einen Zusammenhang. Dies ist die Form, in der wir die Volumenerhaltung mikroskopisch beschreiben können.
Die Physiker kürzen das gerne ab. Wir führen einen Vektor ein, der kein echter Vektor ist, sondern ein Operator:
\[ \vec{\nabla} = \begin{pmatrix} \frac{\partial}{\partial x} \\ \frac{\partial}{\partial y} \\ \frac{\partial}{\partial z} \end{pmatrix} \]
Das ist kein Vektor, denn man kann ihn nur von links an irgendwas ranmultiplizieren. Wir bilden mal das Skalarprodukt mit dem Geschwindigkeitsvektor:
\[ \vec{\nabla} \cdot \vec{u} = \begin{pmatrix} \frac{\partial}{\partial x} \\ \frac{\partial}{\partial y} \\ \frac{\partial}{\partial z} \end{pmatrix} \cdot \begin{pmatrix} u \\ v \\ w \end{pmatrix} = \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z} = 0 \]
Die Volumenerhaltung kann man also ganz kurz schreiben:
\[ \vec{\nabla} \cdot \vec{u} = 0 \]
Später werden wir lernen, wozu man das braucht. Man kann nämlich damit die Vertikalströmung ausrechnen, wenn man die horizontale Strömung kennt. Und die Vertikalströmung ist für die Biologie im Meer sehr relevant.
Wenn die horizontalen Strömungsanteile \(u\) und \(v\) auseinanderströmen,
\[ \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} > 0 \]
nennt man die Strömung (horizontal) divergent. Das geht dann mit einer vertikalen Konvergenz einher, d.h. \(\frac{\partial w}{\partial z} < 0\), die vertikalen Schichten bewegen sich aufeinander zu und werden dünner.
Umgekehrt wird eine Strömung, deren horizontale Strömungsanteile aufeinander zu strömen,
\[ \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} < 0 \]
als (horizontal) konvergent bezeichnet und ist dementsprechend vertikal divergent.
An der Meeresoberfläche kann man konvergente Strömungen manchmal erkennen, weil sich dort Partikel geringer Dichte sammeln. Das können Planktonorganismen sein wie Cyanobakterien, aber auch z.B. Plastikmüll.
