
Um ein paar physikalische Berechnungen anzustellen, wie wir es im Laufe dieser Vorlesung tun wollen, müssen wir erstmal etwas Schulwissen in Mathematik auffrischen.
Eine Zahlenfolge könnte so aussehen:
\[ a_1=3.1, \: a_2=3.01, \: a_3 = 3.001, \ a_4 = 3.0001, \: \dots \]
Wie man sieht, nähert sich diese Folge immer weiter einer bestimmten Zahl an, nämlich der 3.
Man könnte salopp schreiben wollen: \(a_\infty = 3\). Das tut man aber nicht, denn das stimmt nicht. Jedes Glied dieser Zahlenfolge hat ja eine endliche Nummer, es gibt kein \(a_\infty\). Wir schreiben stattdessen:
\[ \lim\limits_{n \rightarrow \infty} a_n = 3 \]
Der Ausdruck \[\lim\] steht für “Limes”, das drückt aus, dass wir einen Grenzübergang machen, von den endlichen Gliedern der Zahlenreihe in die Unendlichkeit. Die 3 ist der Grenzwert der Zahlenfolge.
(Was das genau bedeutet, ist das folgende: Die Reihe kommt immer näher an diesen Grenzwert 3 heran. Wir können uns einen beliebig kleinen Abstand denken, z.B. 0.000001, für jeden noch so kleinen Abstand sind ab irgendwo hinten in der Reihe, ab einem ausreichend großen \(n\), alle Glieder dieser Reihe näher dran an der 3, als dieser Abstand.)
Nun sehen wir uns noch zwei andere Zahlenfolgen an.
\[ b_1=2, \: b_2=4, \: b_3 = 6, \ b_4 = 8, \: \dots \]
Diese Folge hat den Grenzwert “unendlich”.
\[ \lim\limits_{n \rightarrow \infty} b_n = \infty \]
\[ c_1=1, \: c_2=-2, \: c_3 = 3, \ c_4 = -4, \: c_5 = 5, \: \dots \]
Diese Folge hat gar keinen Grenzwert.
Eine Funktion ist eine eindeutige Abbildung. Salopp gesprochen, man steckt was rein, und es kommt was raus, und wenn man dasselbe reinsteckt kommt auch immer dasselbe raus. Ein Beispiel:
\[ f(x) = x^2 \]
Wir stecken 3 rein, und es kommt 9 raus. Allgemein, wir stecken ein \(x\) rein, und es kommt immer und zuverlässig \(x*x\) wieder raus.
Das war der einfachste Fall einer Funktion. Man steckt eine reelle Zahl rein, und es kommt eine reele Zahl wieder raus. Der Mathematiker schreibt: \(f: \mathbb{R} \rightarrow \mathbb{R}\).
Man kann auch mehrere Sachen reinstecken müssen, dann sagt man, die Funktion hat mehrere Argumente. Die folgende Funktion hat zum Beispiel zwei:
\[ f(x,y) = x + y^2 \]
Wenn wir hier 2 und 3 reinstecken, kommt 11 raus. Soweit simpel.
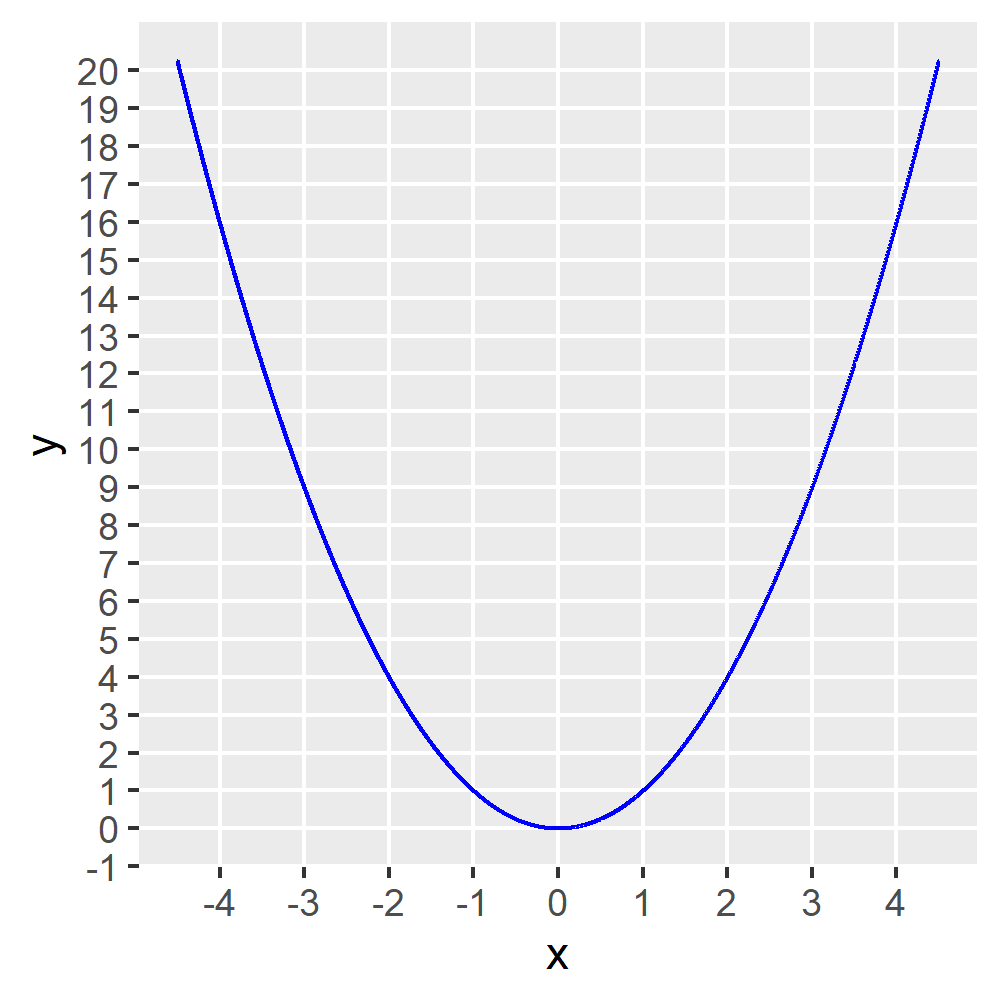
Einfache Funktionen von einem Argument (\(f: \mathbb{R} \rightarrow \mathbb{R}\)) kann man meist gut in einem Funktionsgraph darstellen. Dabei wird das Argument (das man reinsteckt) auf der x-Achse dargestellt und der Funktionswert (das was rauskommt) auf der y-Achse. Die Funktion \(f(x) = x^2\) hätte folgenden Funktionsgraph:

Der folgende Graph stellt keine Funktion dar, denn manche x-Werte haben keinen eindeutigen Funktionswert:
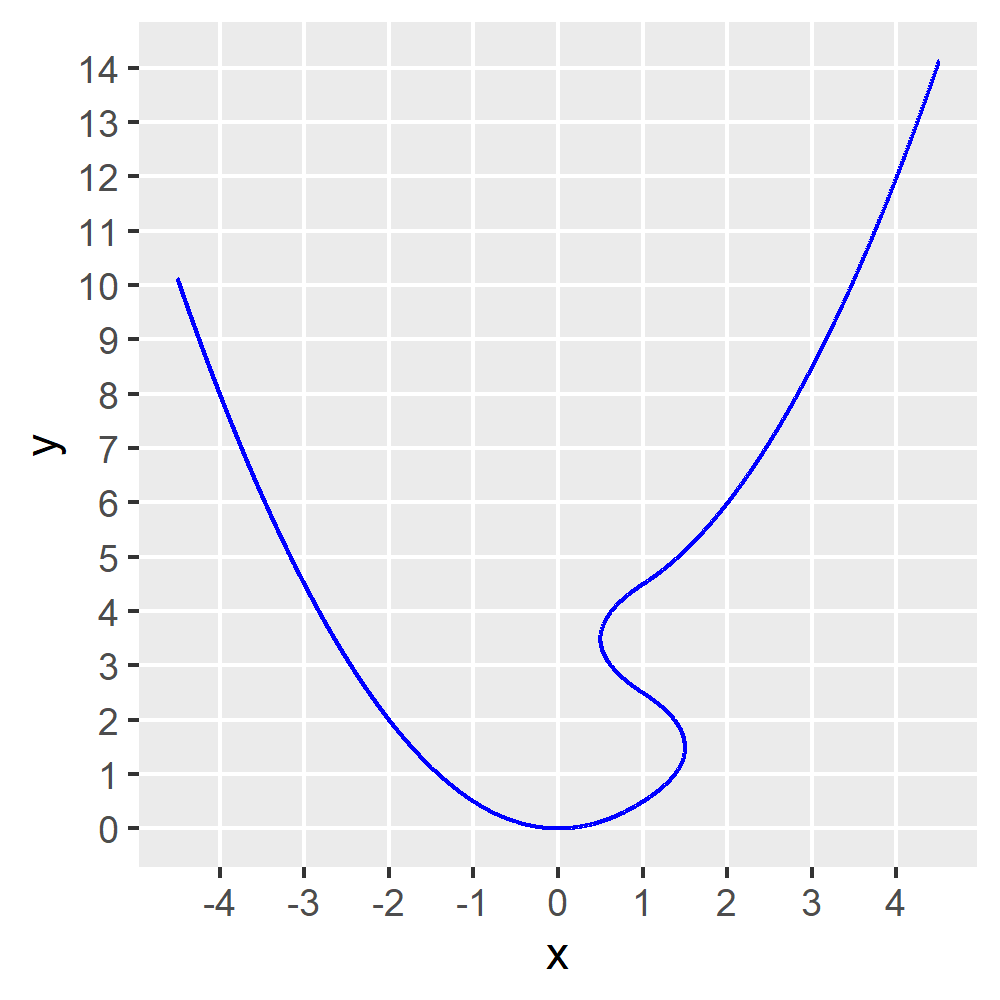
Die Ableitung einer Funktion ist der Anstieg der Tangente an den Funktionsgraphen. Für \(f(x) = x^2\) und \(x = 2\) lässt sich das in der Grafik wie folgt darstellen:
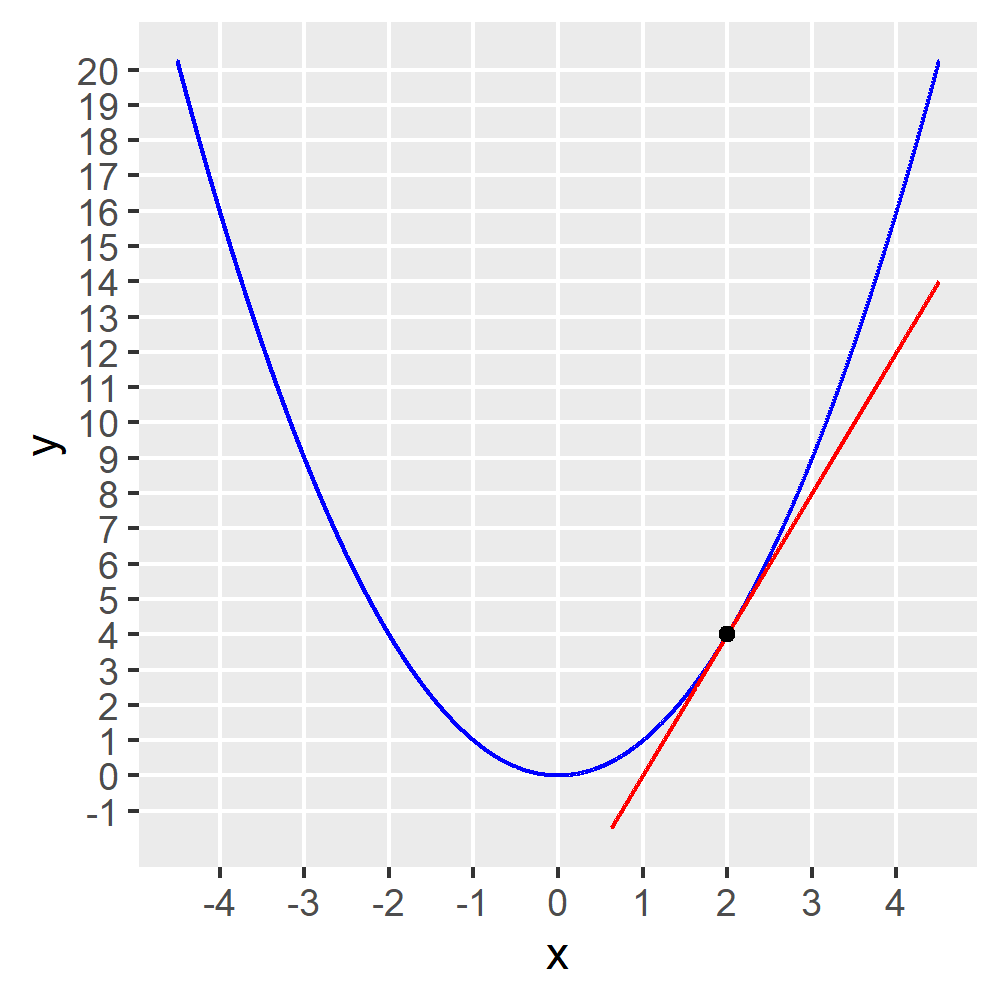
Der Anstieg wäre in diesem Falle 4, wie man durch Kästchen-Zählen herausfindet.
Aber warum wollen wir überhaupt den Anstieg wissen? Das ist wichtig, weil der aussagt, wie schnell eine Größe sich ändert. Also in der Physik meistens entweder * mit der Zeit, wenn die Funktion von der Zeit abhängt, oder * räumlich, wenn die x-Achse eine räumliche Skala darstellt. Am Punkt x=0 ändert sich die Größe zum Beispiel überhaupt nicht.
Den Anstieg können wir uns näherungsweise ausrechnen, indem wir einen kleinen Abstand \(\Delta x\) in x-Richtung betrachten. Für \(\Delta x = 2\) sähe das so aus:
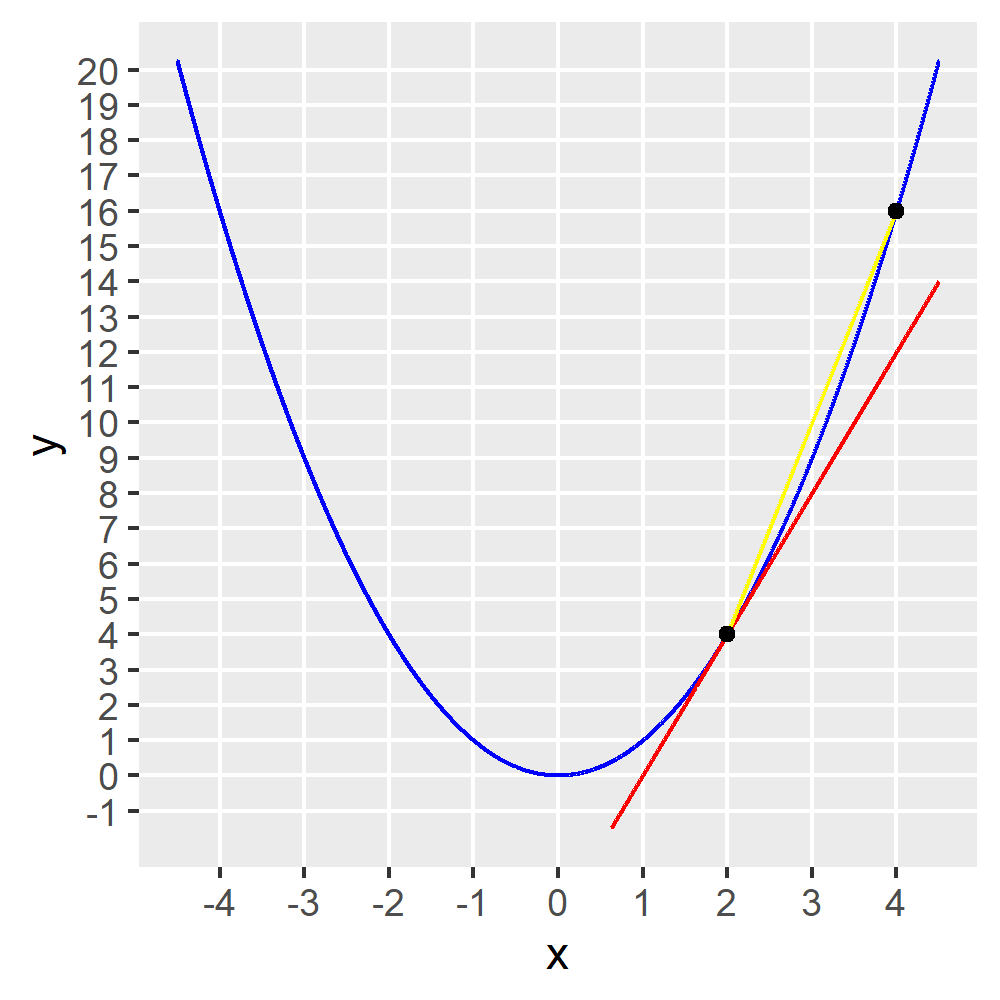
Was wir eigentlich wissen wollen, ist, wie schnell sich die Funktion an der Stelle \(x=2\) ändert. Was wir stattdessen näherungsweise ausrechnen können, ist, wie stark sich die Funktion im Intervall von 2 bis 4 ändert:
\[ f'(x) \approx \frac{f(x+\Delta x) - f(x)}{\Delta x} = \frac{\Delta f}{\Delta x} \]
In unserem Fall ergibt sich:
\[ f'(x) \approx \frac{16 - 4}{2} = 6 \]
Wir könnten aber noch besser approximieren, wenn wir unseren Abstand \(\Delta x\) verkleinern. Sagen wir mal,
\[ \Delta x_1 = 2, \: \Delta x_2 = 1 \]
Das sieht dann so aus:
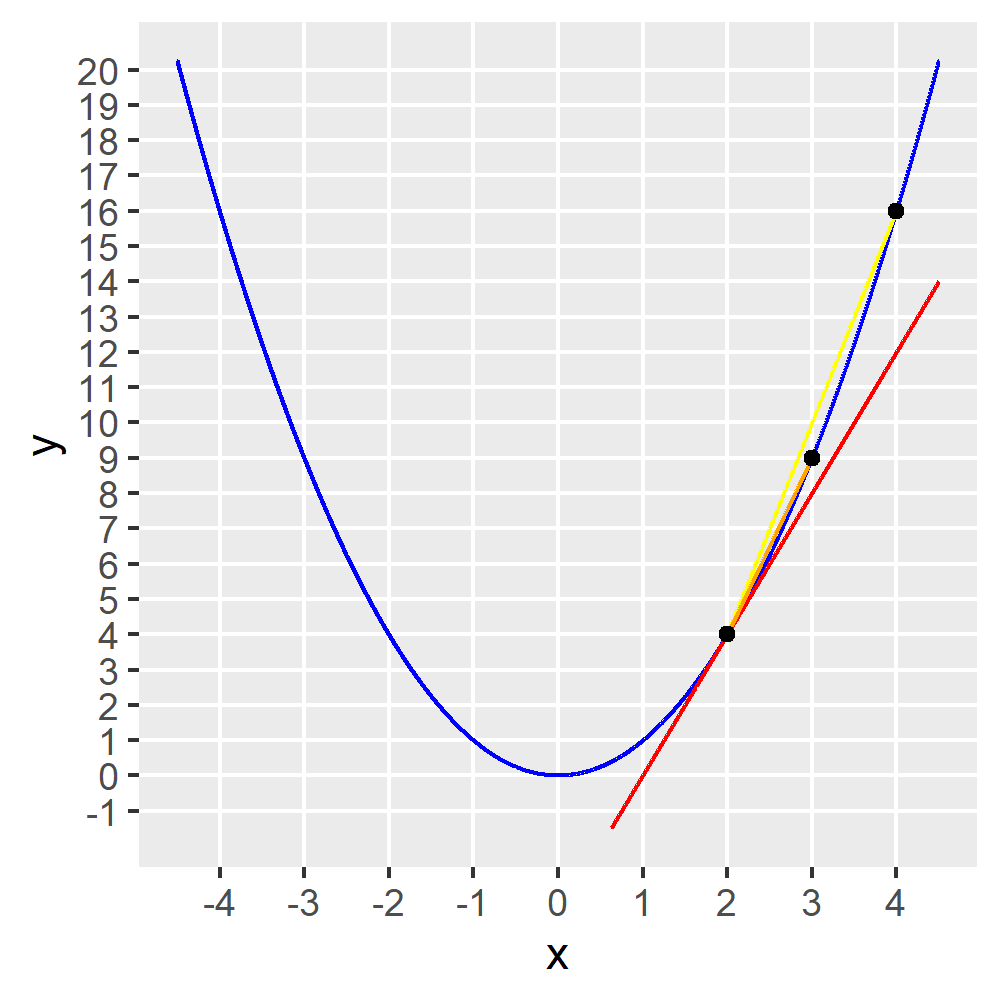
Wir erhalten:
\[ \frac{\Delta f_1}{\Delta x_1} = \frac{16-4}{2} = 6, \: \frac{\Delta f_2}{\Delta x_2} = \frac{9-4}{1} = 5 \]
Das ist der Anfang einer Zahlenfolge. Wir könnten ja immer kleinere Abstände nehmen und immer wieder näherungsweise die Veränderung in diesem immer kleineren Intervall ausrechnen. Dann haben wir die Folge
\[ \frac{\Delta f_1}{\Delta x_1}, \: \frac{\Delta f_2}{\Delta x_2}, \: \frac{\Delta f_3}{\Delta x_3} \: \dots \]
mit immer kleiner werdenden Abständen. Und wenn diese Folge dann einen Grenzwert hat, dann ist das die Ableitung die wir suchen. Darum schreiben wir:
\[ f'(x) = \lim\limits_{\Delta x \rightarrow 0} \frac{\Delta f}{\Delta x} \]
Und die Ableitung wird dann von Physikern lieber so geschrieben:
\[ f'(x) = \frac{\mathrm{d}f}{\mathrm{d}x} \]
Das ist die Infinitesimalrechnung, weil wir von kleinen, aber endlichen Größen dazu übergegangen sind, mit unendlich kleinen Größen zu rechnen.
Wir können die Ableitung natürlich nicht nur an einem Punkt ausrechnen, sondern an jedem beliebigen Punkt. Dann bekommt man wieder eine neue Funktion.
Beispiel:
\[ f(x) = x^2 \: \Rightarrow \: f'(x) = \frac{\mathrm{d}f}{\mathrm{d}x} = 2 \cdot x \]
Dafür haben die Mathematiker Ableitungsregeln hergeleitet. Zum Beispiel diese hier:
\[ f(x) = x^n \: \Rightarrow \: f'(x) = \frac{\mathrm{d}f}{\mathrm{d}x} = n \cdot x^{n-1} \]
Die Infinitesimalrechnung ist gerade in der Ozeanographie oder der Hydrodynamik allgemein sehr nützlich. Nehmen wir zum Beispiel an, wir wollen die Dichte \(\rho\) an einem bestimmten Punkt ausrechnen. Die Dichte ist definiert als Verhältnis zwischen der Masse eines Körpers und seinem Volumen:
\[ \rho = \frac{m}{V} \]
Um unseren Punkt herum können wir uns nun ein kleines Kontrollvolumen \(\Delta V\) denken, z.B. einen Würfel. Dann ist dessen Dichte
\[ \rho = \frac{\Delta m}{\Delta V} \]

und wenn wir den Würfel immer kleiner machen, dann bekommen wir die Dichte an diesem einen Punkt als
\[ \rho = \frac{\mathrm{d} m}{\mathrm{d} V} \]
So können wir kontinuierliche Felder beschreiben. Zum Beispiel sind ja auch die Strömungsgeschwindigkeit oder die Temperatur an jedem Punkt im Meer anders.
Den gleichen Grenzübergang zwischen kleinen und unendlich kleinen Größen macht man nun auch in der Integralrechnung.
Hierbei wollen wir die Fläche unter einem Funktionsgraphen ausrechnen. Und wir werden später noch sehen, warum wir sowas wollen sollten.
Nehmen wir die Funktion \(g(x) = 2\cdot x\). Wir wollen wissen, wie groß die Fläche zwischen \(x=2\) und \(x=4\) ist.
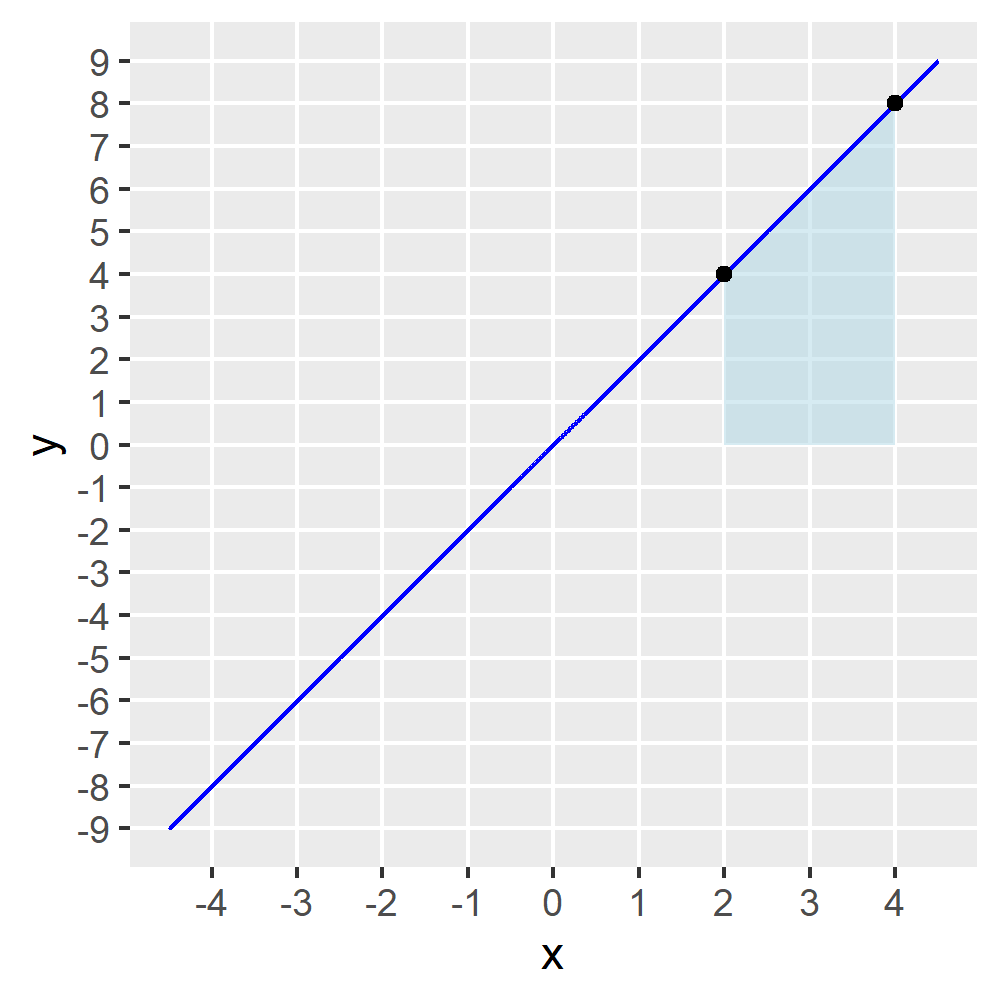
Näherungsweise können wir die als Summe der roten Kästchen ausrechnen:
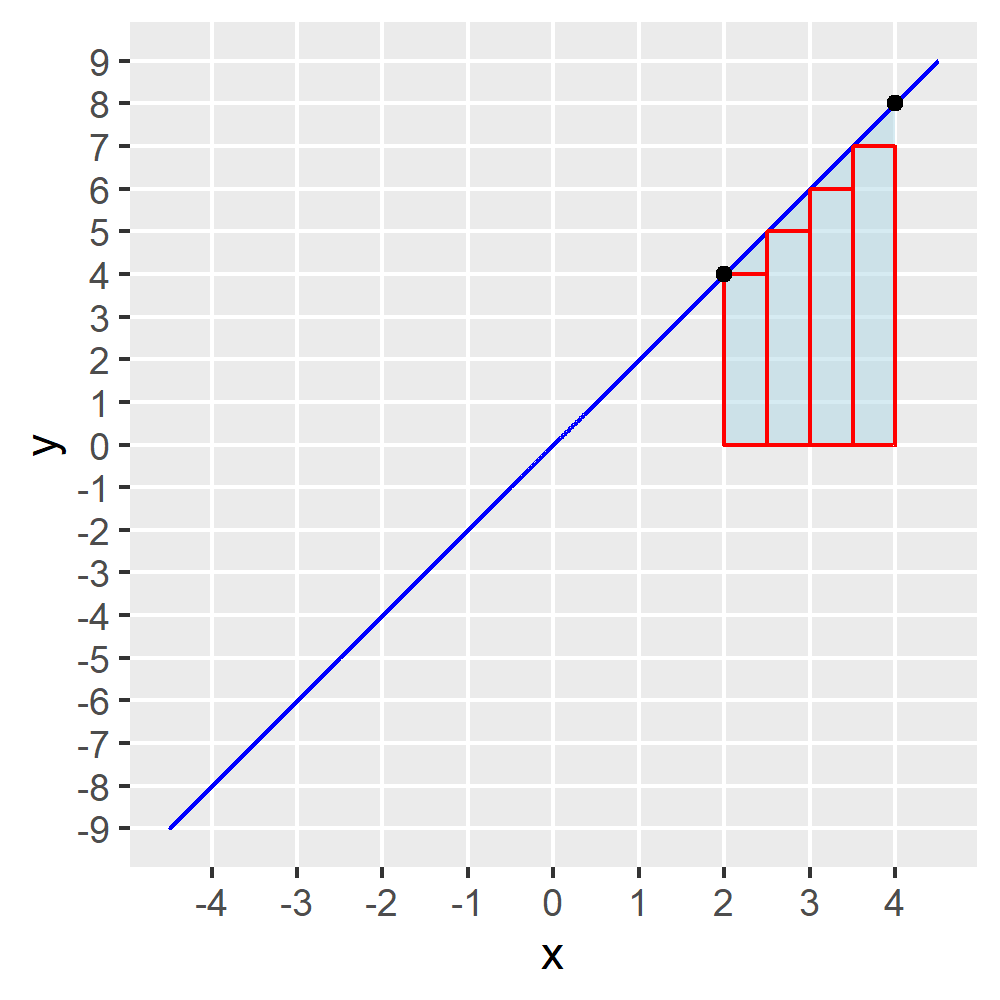
\[ A \approx f(x_1) \cdot \Delta x + f(x_2) \cdot \Delta x + f(x_3) \cdot \Delta x + f(x_4) \cdot \Delta x \]
Jetzt schreiben wir das als Summe:
\[ A \approx \sum\limits_{x_n=2}^{x_n<4} f(x_n) \cdot \Delta x \]
Und jetzt machen wir wieder den Trick, den Grenzübergang, wo wir zu einem unendlich kleines \(\Delta x\) übergehen, das wir dann \(\mathrm{d}x\) nennen. Dann wird aus der Summe ein Integral:
\[ A = \int\limits_{x=2}^{4} f(x) \cdot \mathrm{d} x \]
Wir müssen jetzt nur noch wissen, wie wir Integrale ausrechnen. Dafür gibt’s den Hauptsatz der Differential- und Integralrechnung:
Wenn
\[ f(x) = F'(x) \]
dann gilt
\[ A = \int\limits_{x=x_1}^{x_2} f(x) \cdot \mathrm{d} x = F(x_2) - F(x_1) \]
Mit anderen Worten, integrieren und differenzieren sind genau die Umkehrung voneinander. Wenn wir die Fläche rausbekommen wollen, müssen wir nur die Stammfunktion finden, deren Ableitung unsere Funktion ergibt.
Welch ein Glück: Wir kennen sie schon.
\[ f(x) = 2\cdot x \: \Rightarrow \: F(x) = x^2 \]
Dann testen wir mal:
\[ A = \int\limits_{x=2}^{4} f(x) \cdot \mathrm{d} x = F(4) - F(2) = 4^2 - 2^2 = 16-4 = 12 \]
Wenn wir die Kästchen nachzählen, stimmt das.
Dies war die heutige Wiederholung vom Schul-Mathe.
Wasser bedeckt 70,8% der Erdoberfläche. Den Hauptanteil daran haben 3 Ozeane.
Die Kontinente teilen den Weltozean in:
Das Wasser teilt sich dabei auf wie folgt:
| Anteil | Wassermasse |
|---|---|
| 52% | Pazifik |
| 25% | Atlantik |
| 20% | Indik |
| 3% | Eis, Seen, Flüsse |
Der mit Abstand größte Anteil ist also Salzwasser.
Das liegt vor allem an der Tiefe des Ozeans. Während das Land im Mittel nur 840 m hoch ist, ist der Ozean im Mittel 3729 m tief. Die Ursache dafür sind Unterschiede in der Dichte der Gesteine von kontinentalen und marinen Platten. Wenn diese auf dem Magma schwimmen, dann tauchen sie so tief ein, wie es ihrer Masse entspricht.
Die kontinentalen Platten sind umgeben vom Kontinentalschelf. Das ist eine Region, in der der Ozean (bzw. die Randmeere) relativ flach sind. An der Schelfkante fällt der Meeresboden dann recht abrupt ab.

Der Salzgehalt ist überall im Weltozean fast gleich, er beträgt 35 g/kg. Eine Ausnahme bieten Flussmündungsgebiete und einige Binnenmeere, die Brackwassermeere sind (Ostsee, Schwarzes Meer).
Das Meersalz setzt sich ebenfalls ziemlich gleichmäßig zusammen aus verschiedenen Ionen.
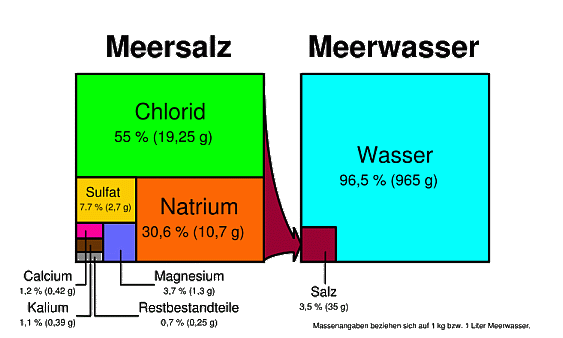
Darüber hinaus enthält das Meerwasser noch weitere Bestandteile, in veränderlichen Anteilen:
Sauerstoff und Stickstoff
CO2 (als CO\(_2\), HCO\(_3^-\) und CO\(_3^{2-}\)), insgesamt dann DIC genannt (dissolved organic carbon)
Silikat (also gelöster Quarzsand)
Nährstoffe (vor allem Nitrat, Phosphat, Ammonium, Eisen)
Deren Anteile sind veränderlich, weil sie Teil des biogeochemischen Kreislaufs sind und von Organismen aufgenommen und abgegeben werden. Obwohl sie sehr wenig vom Massenanteil ausmachen, bestimmen vor allem diese Stoffe das Leben im Meer.
Der Salzgehalt wird heute üblicherweise über die Leitfähigkeit des Wassers gemessen, mithilfe einer CTD-Sonde (conductivity, temperature, depth), denn je mehr Salz und damit je mehr Ionen das Wasser enthält, um so besser leitet es den elektrischen Strom.
Das folgende Bild zeigt, wie die Dichte des Meerwassers und andere Eigenschaften von Temperatur und Salzgehalt abhängen:
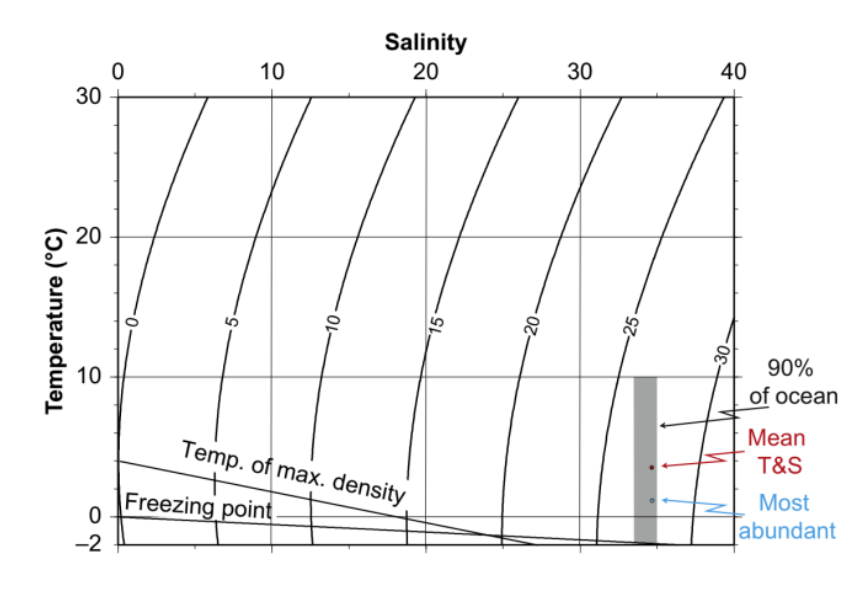
Das Ausrechnen der Dichte erfolgt mithilfe der TEOS-10 Formeln. (Entwickelt von einem ehemaligen Kollegen am IOW.) Die sind für viele verschiedene Software als Paket verfügbar (https://www.teos-10.org/). Wir empfehlen, Python oder R für Berechnungen zu benutzen.
Süßwasser hat seine höchste Dichte bei 4°C. Meerwasser hat nur bis zu einem bestimmten Salzgehalt diese Eigenschaft, dass es eine Dichteanomalie aufweist. Normalerweise wird Meerwasser bei Abkühlung immer dichter, bis es gefriert. Der Gefrierpunkt sinkt dabei mit zunehmendem Salzgehalt.
Das hat erhebliche Unterschiede zwischen Seen und dem Meer bei der Eisbildung zur Folge:
In einem See kühlt, wenn es unter 4°C kalt wird, nur die Oberfläche immer weiter ab. Wenn also eine relativ dünne Oberflächenschicht abgekühlt ist, kann sich bereits Eis bilden. Das Tiefenwasser des Sees verbleibt bei 4°C.
Im Meer (Ausnahme: Brackwassermeere wie die Ostsee) sinkt das kalt werdende Wasser von der Oberfläche immer weiter ab, denn je kälter, um so schwerer. So wird die gesamte Wassersäule immer weiter abgekühlt. Erst wenn das passiert ist (je nach Tiefe kann das sehr lange dauern) bildet sich Meereis. So kann das Meer im Winter viel Wärme an die Atmosphäre abgeben. Bei der Eisbildung wird das übrigbleibende Wasser salziger, denn Meereis enthält viel weniger Salz als das Wasser, aus dem es entstand.
Das kann sogar zur Bildung von Eistrichtern führen, in denen kaltes und salzhaltiges Wasser das umgebende salzärmere gefrieren lässt. Eine eindrucksvolle Aufnahme davon ist einem Team der BBC gelungen.
Im Ozean ist es nun oft so, dass Wassermassen verschiedener Dichte übereinander liegen. Das nennt man dann Schichtung. Je nachdem, warum sich die Dichte zwischen den Schichten ändert sprechen wir von
| sich ändernde Größe | Name der Schichtung | Name der Sprungschicht |
|---|---|---|
| Temperatur | thermische Schichtung | Thermokline |
| Salzgehalt | haline Schichtung | Halokline |
Die Dichte ist immer oben kleiner und unten größer. Wenn sich schwereres Wasser über leichteres schichtet, kommt es sofort zu Konvektion.
Es ist noch folgendes zu beachten:
Eine rein thermische Schichtung kann nur im Brackwasser auch invers sein (oben kalt, unten warm), im Salzwasser nicht.
Eine rein haline Schichtung ist immer oben frischer und unten salziger.
Treten beide in Kombination auf, kann z.B. auch wärmeres salzigeres Wasser unter kälterem frischeren liegen oder umgekehrt, je nachdem welcher Dichteeffekt größer ist.
Die Stärke einer Schichtung kann man mit dem vertikalen Gradienten der Dichte beschreiben:
\[ \frac{\mathrm{d} \rho}{\mathrm{d} z} \]
Üblicher ist es, das nochmal durch die Dichte selbst zu teilen und mit der Fallbeschleunigung \(g\) zu multiplizieren:
\[ N^2 = \frac{g \cdot \frac{\mathrm{d} \rho}{\mathrm{d} z}}{\rho} \]
Denn dann bekommt man die Einheit \(\mathrm{s}^{-2}\). Die Größe \(N\) wird als Brunt–Väisälä-Frequenz bezeichnet. Sie beschreibt, wie schnell ein Wasserpartikel, das innerhalb der Schichtung nach oben oder unten ausgelenkt wurde, aufgrund seiner höheren (oder niedrigeren Dichte) wieder herumpendeln würde.
Biologisch ist wichtig, dass zwischen verschiedenen Dichteschichten meist kein oder sehr wenig Austausch von z.B. Nährstoffen oder Sauerstoff stattfindet. Dadurch kann sich dann Anoxie (Sauerstoffarmut) bilden.